Giúp mình câu 14, 15 với.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
14.
Hàm số ko xác định tại \(x=-1,x=2\) nên gián đoạn tại \(x=-1,x=2\)
A đúng
15.
\(\lim\limits_{x\rightarrow1^-}\dfrac{2x+1}{x-1}=-\infty\)
(Do \(\lim\limits_{x\rightarrow1^-}\left(2x+1\right)=3>0\) và \(x-1< 0\) khi \(x< 1\))
11 tháng 3 2023
Câu 14:
\(n_{H_2O}=\dfrac{3,6}{18}=0,2\left(mol\right)\Rightarrow n_H=0,2.2=0,4\left(mol\right)\)
Có: mC + mH = 5,2 (g) ⇒ mC = 5,2 - 0,4.1 = 4,8 (g)
\(\Rightarrow n_{CO_2}=n_C=\dfrac{4,8}{12}=0,4\left(mol\right)\)
A: CnH2n-2
⇒ nA = nCO2 - nH2O = 0,4 - 0,2 = 0,2 (mol)
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_A}=2\)
→ A là C2H2.
→ Đáp án: B
Câu 15:
X: CnH2n-2
\(\Rightarrow\dfrac{2n-2}{12n+2n-2}=0,11111\Rightarrow n=4\)
→ X là C4H6.
CTCT: \(CH\equiv C-CH_2-CH_3\)
\(CH_3-C\equiv C-CH_3\)
→ Đáp án: B
17 tháng 2 2023
Câu 14:
Ta có: \(n_{C_2H_4}+n_A=\dfrac{3,36}{22,4}=0,15\left(1\right)\)
m bình tăng = mC2H4 = 1,4 (g) \(\Rightarrow n_{C_2H_4}=\dfrac{1,4}{28}=0,05\left(mol\right)\) (2)
Từ (1) và (2) \(\Rightarrow n_A=0,1\left(mol\right)\)
Gọi CTPT của A là CnH2n+2.
Có: \(n_{CO_2}=\dfrac{8,8}{44}=0,2\left(mol\right)\)
\(\Rightarrow n=\dfrac{n_{CO_2}}{n_A}=2\)
Vậy: A là C2H6.
→ Đáp án: A.
Câu 15:
Ta có: \(n_{CO_2}=n_{H_2O}=x\left(mol\right)\)
\(n_{O_2}=\dfrac{13,44}{22,4}=0,6\left(mol\right)\)
BTNT O, có: \(2n_{CO_2}+n_{H_2O}=2n_{O_2}\)
\(\Rightarrow2x+x=2.0,6\Leftrightarrow x=0,4\left(mol\right)\)
BTNT C, có: \(n_{CaCO_3}=n_{CO_2}=0,4\left(mol\right)\)
\(\Rightarrow m_{CaCO_3}=0,4.100=40\left(g\right)\)
→ Đáp án: C
2 tháng 1
Câu 13:
1:
a: \(2x^2+2x=2x\cdot x+2x\cdot1=2x\left(x+1\right)\)
b: \(9x^2-4y^2\)
\(=\left(3x\right)^2-\left(2y\right)^2\)
=(3x-2y)(3x+2y)
2:
\(\dfrac{xy+2x+1}{xy+x+y+1}+\dfrac{yz+2y+1}{yz+y+z+1}+\dfrac{zx+2z+1}{zx+z+x+1}\)
\(=\dfrac{xy+2x+1}{\left(y+1\right)\left(x+1\right)}+\dfrac{yz+2y+1}{\left(z+1\right)\left(y+1\right)}+\dfrac{z\left(x+2\right)+1}{\left(z+1\right)\left(x+1\right)}\)
\(=\dfrac{\left(xy+2x+1\right)\left(z+1\right)+\left(yz+2y+1\right)\left(x+1\right)+\left(xz+2z+1\right)\left(y+1\right)}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{xyz+xy+2xz+2x+z+1+xyz+yz+2xy+2y+x+1+\left(xz+2z+1\right)\left(y+1\right)}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{2xyz+3xy+2xz+3x+z+2+yz+2y+x+xyz+xz+2zy+2z+y+1}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{3xyz+3xy+3xz+3yz+3x+3z+3y+3}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{3\left(xyz+xy+xz+yz+x+z+y+1\right)}{\left(xy+x+y+1\right)\left(z+1\right)}\)
=3
Câu 14:
1:
f(0)=0+5=5
2:
Vì hệ số góc của y=ax+b là -1 nên a=-1
=>y=-x+b
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3
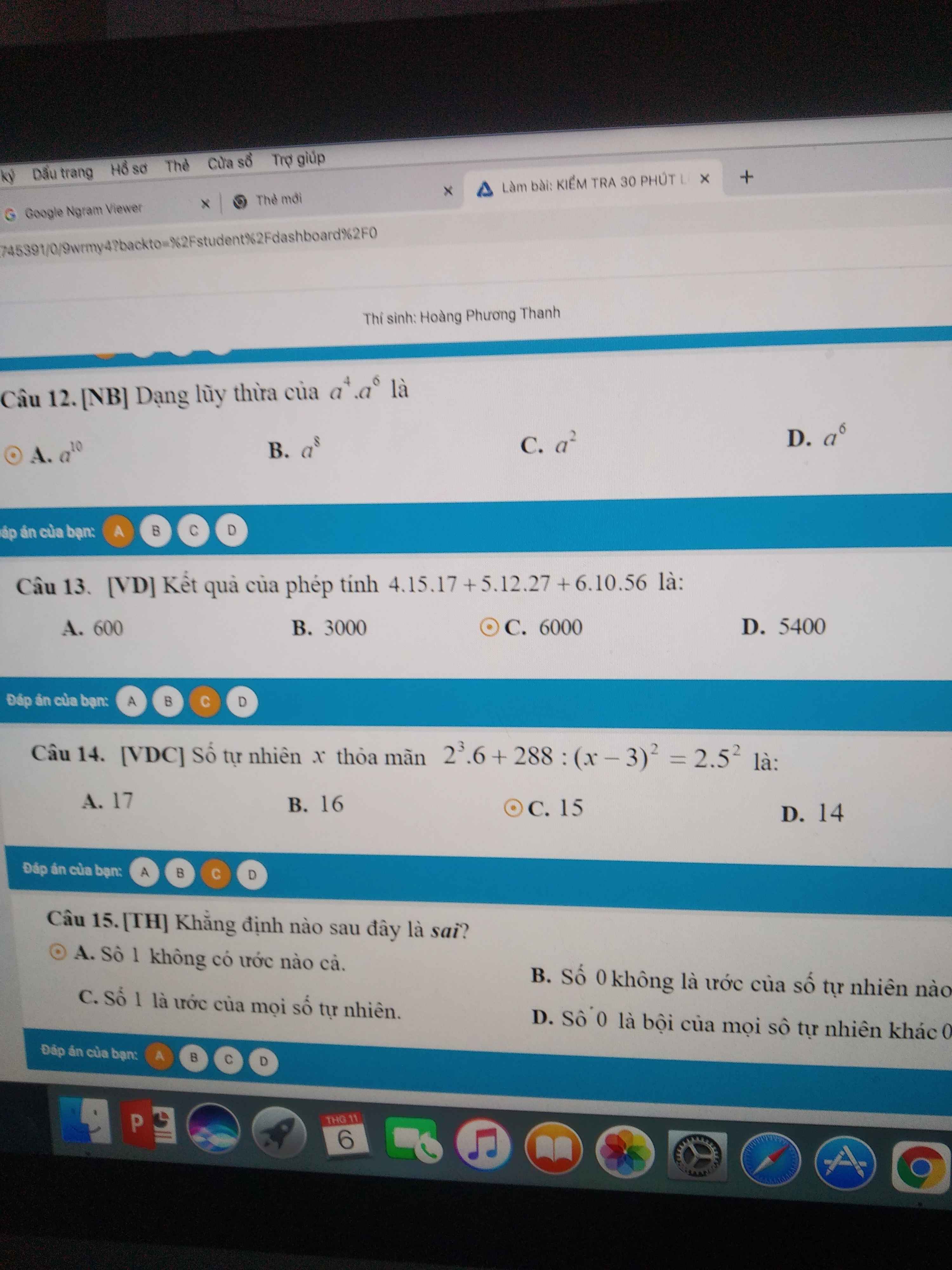
giúp mình câu 14 15 16 17
DT
2
DN
1
TH
1