Cho 6 điểm phân biệt trong không có bất cứ 3 điểm nào thẳng hàng. Có bao nhiêu tam giác có 3 đỉnh là 3 trong số 6 điểm đã cho.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 12 2021
Chọn 3 điểm trong 15 điểm có: \(C^3_{15}\)(cách chọn)
Chọn 3 điểm trong 6 điểm thẳng hàng có:\(C^3_6\)(cách)
=>Số tam giác được tạo thành từ 15 điểm đã cho là: \(C^3_{15}-C^3_6\)(tam giác)
CM
30 tháng 5 2018
Cứ chọn 3 điểm không thẳng hàng bất kì ta được một tam giác.
Việc lập các tam giác chính là chọn 3 điểm trong tập hợp 6 điểm đã cho và chính là tổ hợp chập 3 của 6.
Vậy có:
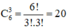cách lập.
CM
25 tháng 3 2019
Đáp án là B
Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.
Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).
Như vậy, ta có C 6 3 = 20 tam giác.
LT
3 tháng 4 2017
Mỗi tập con gồm 3 điểm (không phân biệt thứ tự) của tập hợp 6 điểm đã cho xác định duy nhất một tam giác. Từ đó ta có: số tam giác có thể lập được (từ 6 điểm đã cho) là:
C36 = = 20 (tam giác)
Mà có 6 điểm nên có : 6.5=30 đoạn thẳng
Như thế mỗi đoạn thẳng sẽ được tính 2 lần nên có số đoạn thẳng thực sự là : 30:2=15 đoạn thẳng
Mà có 15 đoạn thẳng nên có : 15.4= 60(tam giác)
Như thế mỗi tam giác sẽ được tính 3 lần nên có số tam giác thực sự là : 60:3 = 20 tam giác
Vậy có 20 tam giác
Chúc bạn học tốt nhé !!!