Cho \(\Delta\)ABC vuông cân tại A. Kẻ tia phân giác của góc A cắt BC tại H. Trên tia AB, AC lấy điểm N và M sao cho BN=AM. Chứng minh rằng:
a, \(\Delta\)AHN=\(\Delta\)CHM
b,\(\Delta\)AHM=\(\Delta\)NHN
c,\(\Delta\)MHN vuông cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2023
a: Xet ΔAHN và ΔCHM có
AH=CH
góc HAN=góc HCM
AN=CM
=>ΔAHN=ΔCHM
b: Xet ΔAHM và ΔBHN co
AH=BH
góc HAM=góc HBN
AM=BN
=>ΔAHM=ΔBHN
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
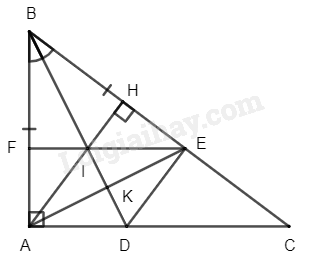
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:
\(BA = BE\) (gt)
\(\widehat {{\rm{ABD}}} = \widehat {{\rm{ EBD}}}\) (do \(BD\) là phân giác)
\(BD\) chung
Suy ra \(\Delta ABD = \Delta EBD\) (c-g-c)
b) Vì \(\Delta ABD = \Delta EBD\) (cmt)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{BED}}} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DE \bot BC\)
Mà \(AH \bot BC\) (gt)
Suy ra \(AH\) // \(DE\)
Suy ra \(ADEH\) là hình thang
Mà \(\widehat {{\rm{DEB}}} = 90\) (cmt)
Suy ra \(ADEH\) là hình thang vuông
c)
Gọi \(K\) là giao điểm của \(AE\) và \(AD\)
Suy ra \(BK\) là phân giác của \(\widehat {{\rm{ABC}}}\)
Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )
Suy ra \(BK\) cũng là đường cao
Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\)
Suy ra \(I\) là trực tâm của \(\Delta ABE\)
Suy ra \(EF \bot AB\)
Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\))
Suy ra \(AC\) // \(EF\)
Suy ra \(ACEF\) là hình thang
Mà \(\widehat {{\rm{CAE}}} = 90^\circ \)(gt)
Suy ra \(ACEF\) là hình thang vuông
4 tháng 5 2019
Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
4 tháng 5 2019
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
1 tháng 4 2020
a)+) Ta có
AB = AC (do ∆ABC cân tại A )
BN = CM (gt)
=> AB - BN = AC - AM
=> AN = CM
+) Lại có ABC = ACB = 45° ( do ∆ ABC vuông cân tại A)
BAH = CAH = BAC /2 = 90°/2= 45° ( do AH là pg BAC)
=> ABC = BAH = ACB = CAH = 45°
=> ∆ ABH cân tại H và ∆ ACH cân tại H
=> HA= HB , HA = HC
+) Xét ∆ NAH và ∆ MCH có
NA = MC (cmt)
NAH = MCH (= 45°)
AH = CH (cmt)
=> ∆NAH = ∆MCH (c.g.c)
b)+) Xét ∆ AHM và ∆BHN có
AH = BH (cmt)
HAC = HAB =45°
AM = BN (gt)
=> ∆AHM = ∆BHN (c.g.c)
=> HM = HN (1) (2cạnh t/ứ)
Và AHM = BHN (2) (2góc t/ứ)
c) +) Xét ∆ABH và ∆ACH có
AB = AC (do ∆ ABC cân tại A)
HAB = HAC (do AH là pg BAC)
AH : cạnh chung
=> ∆AHB = ∆ AHC (c.g.c)
=> AHB = AHC (2góc t/ứ )
Mà AHB + AHC = 180° (kề bù )
=> AHB = AHC = 90°
Hay AHN + NHB = AHB = 90° (3)
Từ (2) và (3) => NHA + AHN = 90°
=> NHM = 90° (4)
Từ (1) và (4) => ∆ NHM vuông cân
Bài dài wá
1 tháng 4 2020
a) Ta có: ΔABC vuông cân tại A(gt)
⇒AB=AC và \(\widehat{B}=\widehat{C}=45^0\)(số đo của các cạnh và các góc trong ΔABC vuông cân tại A)
mà \(\widehat{CAH}=\widehat{BAH}=\frac{\widehat{BAC}}{2}=\frac{90^0}{2}=45^0\)(AH là tia phân giác của \(\widehat{BAC}\))
nên \(\widehat{B}=\widehat{C}=\widehat{CAH}=\widehat{BAH}\)
Ta có: AN+NB=AB(N nằm giữa A và B)
AM+CM=AC(M nằm giữa A và C)
mà AB=AC(cmt)
và AM=NB(gt)
nên AN=CM
Ta có: ΔABC vuông cân tại A(gt)
mà AH là đường phân giác ứng với cạnh đáy BC(gt)
nên AH cũng là đường trung tuyến, đường cao ứng với cạnh BC(định lí tam giác cân)
⇒H là trung điểm của BC
Ta có: ΔABC vuông cân tại A(gt)
mà AH là đường trung tuyến ứng với cạnh huyền BC(cmt)
nên \(AH=\frac{BC}{2}\)(định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CH=HB=\frac{BC}{2}\)(H là trung điểm của BC)
nên AH=CH=BH
Xét ΔAHN và ΔCHM có
AN=CM(cmt)
\(\widehat{HAN}=\widehat{C}\)(\(\widehat{HAB}=\widehat{C}\), N∈AB)
AH=CH(cmt)
Do đó: ΔAHN=ΔCHM(c-g-c)
b) Ta có: ΔAHN=ΔCHM(cmt)
⇒HN=MH(hai cạnh tương ứng)
Xét ΔAHM và ΔBHN có
HM=HN(cmt)
AM=BN(gt)
AH=BH(cmt)
Do đó: ΔAHM=ΔBHN(c-c-c)
KV
2 tháng 5 2023
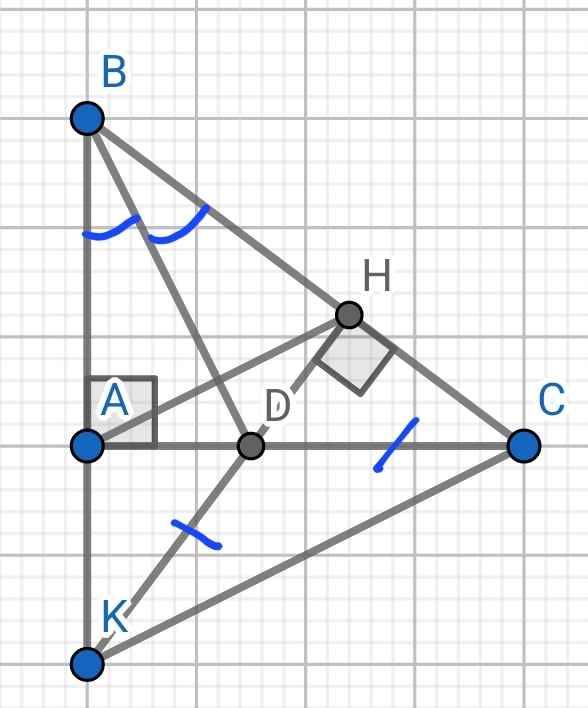
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng
21 tháng 3 2023
a: Xet ΔABD vuông tại B và ΔAHD vuông tại H có
AD chung
góc BAD=góc HAD
=>ΔABD=ΔAHD
b; AB=AH
DB=DH
=>AD là trung trực của BH
c: Xet ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
góc BDI=góc HDC
=>ΔBDI=ΔHDC
=>DI=DC
=>ΔDIC cân tại D
d: Xét ΔAIC có AB/BI=AH/HC
nên BH//IC
e: AD vuông góc BH
BH//IC
=>AD vuông góc IC
câu này thì em ko biết vì em mới học lớp6
Bài làm
a) Vì tam giác ABC vuông cân ở A
Mà AH là phân giác
=> AH là trung tuyến.
=> AH = BH = HC
=> Tam giác AHC cân tại H
=> AH = HC
=> \(\widehat{HAC}=\widehat{HCA}\)
Mà \(\widehat{HAB}=\widehat{HAC}\)( Do AH phân giác )
=> \(\widehat{HCA}=\widehat{HAB}\)
Ta có: AN + NB = AB
AM + MC = AC
mà AB = AC, BN = AM
=> AN = MC
Xét tam giác AHN và tam giác CHM có:
AN = MC ( cmt )
\(\widehat{HCA}=\widehat{HAB}\)( cmt )
AH = HC ( cmt )
=> Tam giác AHN = tam giác CHM ( c.g.c)
b) Vì tam giác AHN = tam giác CHM ( cmt )
=> NH = HM
Vì AH trung tuyến
=> BH = HC
Xét tam giác AHM và tam giác NHB có:
NH = HM ( cmt )
BN = AM ( gt )
HB = HC ( cmt )
=> Tam giác AHM = tam giác NHB ( c.c.c )