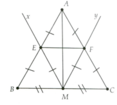
Cho tam giác đều ABC, M là trung điểm của BC. Vẽ tia Mx // AC cắt AB tại E và tia My // AB cắt AC tại F. Chứng minh rằng:
a) Tam giác AEF là tam giác đều
b) EF // BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 4 2020
a) Có Mx//AC và Mx giao AB tại E => E là trung điểm AB (1) => \(AE=BE=\frac{AB}{2}\)(*)
Lại có My//AB và My giao AC tại F => F là trung điểm AC (2) => \(AF=FC=\frac{AC}{2}\)(**)
Từ (1)(2) => EF//BC (câu b)
=> \(EF=\frac{1}{2}BC\)(***)
AB=BC=AC (\(\Delta\)ABC đều) (****)
Từ (*)(**)(***)(****) => AE=AF=EF => \(\Delta\)AEF đều (đpcm)
CM
29 tháng 12 2018
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
