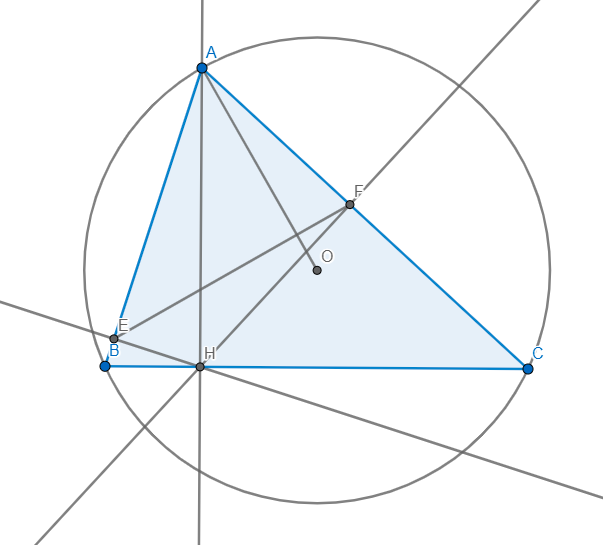
*Bài 1: Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Vẽ đường cao AH (H thuộc cạnh BC). Vẽ HE vuông góc với AB (E thuộc AB), HF vuông góc với AC (F thuộc AC).
a) Chứng minh rằng AEHF là tứ giác nội tiếp
b) Chứng minh rằng ABC + HFE = 90°
c) Gọi M là giao điểm của BF và HE, N là giao điểm của HF và CE.
Chứng minh rằng MN song song với BC.
* Bài 2: Cho tam giác ABC có A= 60°. Các điểm 0, I lần lượt là tâm đường tròn ngoại tiếp, nội tiếp tam giác. Chứng minh rằng bốn điểm B, 0, I, C cùng thuộc một đường tròn.