Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
nếu câu a và b bạn đã biết cách giải rồi thì mình xin phép gợi ý câu c :)
vì có lực cản cơ năng của vật không bảo toàn và công của lực cản bằng độ biến thiên cơ năng: \(A=W_2-W_1=\dfrac{1}{2}mv_2^2+mgz_2-\left(\dfrac{1}{2}mv_1^2+mgz_1\right)\)
rồi bạn giải nốt
Chọn gốc thế năng tại độ cao 5m so với mặt đất.
\(\Rightarrow h=10-5=5cm\)
Cơ năng vật:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot0,4\cdot20^2+0,4\cdot10\cdot5=100J\)
Ta có
\(W=W_đ+W_t\\ \Leftrightarrow mgh+\dfrac{mv^2}{2}=0,4.10.10+\dfrac{0,4.20^2}{2}\\ =120\left(J\right)\)
a, \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot5^2=1,25\left(J\right)\)
\(W_t=mgz=0,1\cdot10\cdot2=2\left(J\right)\)
\(W=W_đ+W_t=1,25+2=3,25\left(J\right)\)
b, Gọi vị trí 1 là vị trí vật đạt được độ cao cực đại
Khi vật đạt được độ cao cực đại z1 thì v1 = 0
\(W_1=W_{đ_1}+W_{t_1}=\dfrac{1}{2}mv_1^2+mgz_1=mgz_1\)
Áp dụng ĐLBTCN: \(W=W_1\Leftrightarrow W=mgz_1\Leftrightarrow z_1=\dfrac{W}{mg}=\dfrac{3,25}{0,1\cdot10}=3,25\left(m\right)\)
Phương trình chuyển động:
+ Theo phương Ox: x = v 0 t (1)
+ Theo phương Oy: y = 1 2 g t 2 (2)
Phương trình quỹ đạo (thay t ở (1) vào (2)): y = g 2 v 0 2 x 2
=> phương trình quỹ đạo của vật ném ngang trong trường hợp trên: y = g 2 v 0 2 x 2 = 10 2.10 2 = 0 , 05 x 2
Đáp án: C
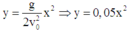
a. Áp dụng ĐL bảo toàn cơ năng cho vật tại vị trí ném và mặt đất
\(\frac{1}{2}mv_0^2+mgh=\frac{1}{2}mv_{max}^2\)
\(\Rightarrow v_0^2=v_{max}^2-2gh=18^2-2.10.16=4\)
\(\Rightarrow v_0=2\) m/s
b. Tại vị trí động năng bằng thế năng có
\(W=2W_t\)
\(\Rightarrow\frac{1}{2}mv_{max}^2=2mgh\)
\(\Rightarrow h=\frac{1}{4g}v_{max}^2=8,1\) m