Cho một tam giác vuông tại A (AC>AB). M,N,K lần lượt là trung điểm AB,BC,AC. Từ M kẻ đường song song với BK, đường thẳng này cắt NK tại E.a)Tứ giác AMNK là hình gì ?Vì sao? b)CMinh hình BMEK là hình bình hành c)CMinh tứ giác ANCE là hình thoi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 3 2022
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
KV
16 tháng 12 2023
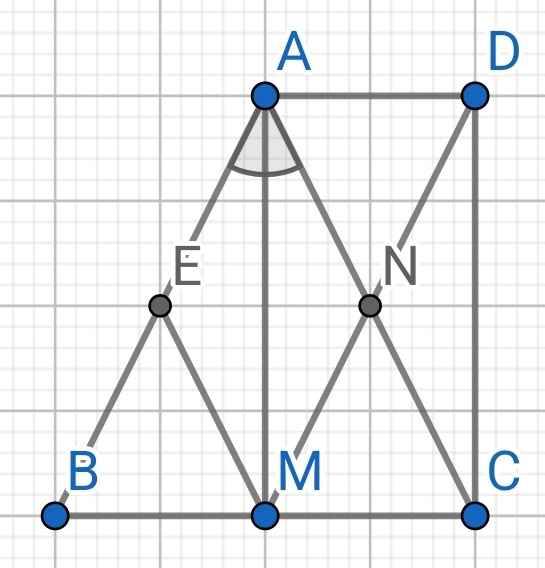a) Do MN // AB (gt)
⇒ MN // AE
Do ME // AC (gt)
⇒ ME // AN
Do AM là tia phân giác của ∠BAC (gt)
⇒ AM là tia phân giác của ∠EAN
Xét tứ giác AEMN có:
MN // AE (cmt)
ME // AN (cmt)
⇒ AEMN là hình bình hành
Mà AM là tia phân giác của ∠EAN (cmt)
⇒ AEMN là hình thoi
b) Do D là điểm đối xứng của M qua N (gt)
⇒ N là trung điểm của DM
∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
∆ABC có:
M là trung điểm của BC (cmt)
MN // AB (gt)
⇒ N là trung điểm của AC
Tứ giác ADCM có:
N là trung điểm của DM (cmt)
N là trung điểm của AC (cmt)
⇒ ADCM là hình bình hành
⇒ AD // CM
⇒ AD // BM
Do MN // AB (gt)
⇒ MD // AB
Tứ giác ADMB có:
MD // AB (cmt)
AD // BM (cmt)
⇒ ADMB là hình bình hành
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 9 2023
a/
Ta có
FA=FC; GB=GC => GF là đường trung bình của tg ABC
=> GF//AB Mà \(AB\perp AC\)
\(\Rightarrow GF\perp AC\)
=> AEGF là hình thang vuông tại A và F
b/
EI//BF (gt)
GF//AB => FI//BE
=> BEIF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Ta có GF là đường trung bình của tg ABC \(\Rightarrow GF=\dfrac{1}{2}AB\)
BEIF là hbh (cmt) =>FI=EB
Mà \(EA=EB=\dfrac{1}{2}AB\)
=> GF=FI
Ta có
FA=FC
=> AGCI là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Mà \(GF\perp AC\Rightarrow GI\perp AC\)
=> AGCI là hình thoi (Hình bình hành có 2 đường chéo vuông góc là hình thoi)
d/
Để AGCI là hình vuông \(\Rightarrow AG\perp BC\) => AG là đường cao của tg ABC
Mà GB=GC => AG là đường trung tuyến của tg ABC
=> tg ABC là tg cân tại A (Tam giác có đường cao và đồng thời là đường trung tuyến là tg cân)
Mà \(\widehat{A}=90^o\) (gt)
=> Đk để AGCI là hình vuông thì tg ABC phải là tg vuông cân tại A
19 tháng 12 2021
a: Xét tứ giác AEGK có
GK//AE
GK=AE
Do đó: AEGK là hình bình hành
mà \(\widehat{KAE}=90^0\)
nên AEGK là hình chữ nhật