các bac giúp em với ạ
bài 1
1)phân tích đa thức sau thành nhân tử
a)\(^{x^2-xy}\)
b)\(x^2+2xy+y^2-4\)
2)rút gọn biểu thức sau (2x-1)(2x+1)+4x(1-x)
3)tìm giá trị x biết \(x^2-6x+5=0\)
bài 2 thực hiện phép tính
a)\(\frac{1-2y}{6y^2}+\frac{10y-1}{6y^2}\) c)\(\left(\frac{x+1}{x^2-2x+1}+\frac{1}{x-1}\right):\frac{x}{x-1}-\frac{2}{x-1}\)
b)\(\frac{5x+y^2}{x^2y}-\frac{5y-x^2}{xy^2}\) d)\(\left(x^3-x^2-7x+3\right):\left(x-3\right)\)

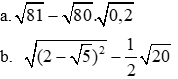
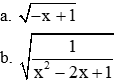
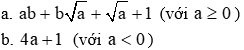
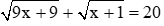
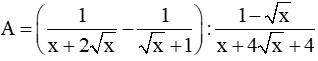
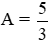
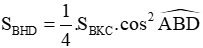
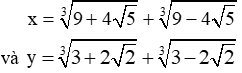
.các bác giúp em với ạ,em cảm ơn trc ạ
bài 1 :
1,
a, x^2 - xy = x(x - y)
b, x^2 + 2xy + y^2 - 4
= (x + y)^2 - 2^2
= (x + y + 2)(x + y - 2)
2,
(2x-1)(2x+1)+4x(1-x)
= 4x^2 - 1 + 4x - 4x^2
= 4x - 1
3, x^2 - 6x + 5 = 0
<=> x^2 - x - 5x + 5 = 0
<=> x(x - 1) - 5(x - 1) = 0
<=> (x - 5)(x - 1) = 0
<=> x = 5 hoặc x = 1