Cho điểm A nằm ngoài đường (O;R), vẽ AB là tiếp tuyến của đường tròn (O) (B là tiếp điểm).Kẻ dây BC vuông góc với OA tại H.
a) Chứng minh AC là tiếp tuyến của đường tròn (O)
b) Kẻ đường kính CD của đường tròn (O).Chứng minh BD//OA
c) Tính OA.OH theo R.
d) Giả sử OH< R/2. Cho M là điểm di động trên đoạn thẳng BC, qua A vẽ đường thẳng vuông góc đường thẳng OM tại N.Tìm giá trị nhỏ nhất của (4.OM + ON)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)

Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)
Qua điểm thứ nhất: 0 tam giác
Qua điểm thứ 2: Thêm 1 tam giác
Qua điểm thứ 3: Thêm 2 tam giác
Qua điểm thứ 4: Thêm 3 tam giác
...
...
Qua điểm thứ 10: Thêm 9 tam giác
Tổng số tam giác là: 0+1+2+3+...+9 = 45 (tam giác)
Đáp số: 45 (tam giác)

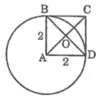
OA = 2 < 2 nên điểm O và A nằm trong (A; 2)
AB = 2 nên điểm B nằm trên (A; 2)
AD = 2 nên điểm D nằm trên (A; 2)
AC = 2 2 > 2 nên điểm C nằm ngoài (A; 2)



Giải :
a, Ta có :
OH vuông góc BC tại trung điểm
Xét Δ OBC có :
OB = OC ( = R)
=> Δ OBC cân tại O
=> \(\widehat{BOH}=\widehat{COH}\)
Xét Δ ABO và Δ ACO có :
OB = OC ( =R)
\(\widehat{BOA}=\widehat{COA}\)
OA : chung
=> Δ ABO = Δ COA ( c- g - c)
=> \(\widehat{ABO}=\widehat{ACO}\)
=> OC vuông góc với AC
mà C thuộc ( O ).
=> AC là tiếp tuyến của đường tròn ( O ). ( đpcm)
b, Xét đường tròn ( O ), ta có :
\(\widehat{CBD}\)= \(90^0\)( góc nội tiếp chắn nửa đường tròn )
=> BD vuông góc với BC
Mà OA vuông góc với BC ( gt)
=> OA// BD (đpcm).
c, Áp dụng hệ thức lượng vào Δ ABO có :
\(OB^2=OH.OA\)
mà OB = R
=> OH. OA = \(R^2\)
Mong rằng có thể giúp bạn ! Mik chỉ biết làm đến câu c mà thôi !