Giải phương trình: x2 + 2019x = 2020
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(DK:x\ge\frac{2020}{2019}\)
PT\(\Leftrightarrow\left(\sqrt{2020x-2019}-\sqrt{2019x-2020}\right)+2019\left(x+1\right)=0\)
\(\Leftrightarrow\frac{x+1}{\sqrt{2020x-2019}+\sqrt{2019x-2020}}+2019\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\frac{1}{\sqrt{2020x-2019}+\sqrt{2019x-2020}}+2019\right)=0\)
:)
https://olm.vn/thanhvien/chibiverycute là con chó
https://olm.vn/thanhvien/chibiverycute là con chó
https://olm.vn/thanhvien/chibiverycute là con chó
https://olm.vn/thanhvien/chibiverycute là con chó
https://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chó
https://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóvhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chóhttps://olm.vn/thanhvien/chibiverycute là con chó

với \(x\ge\frac{2020}{2019}\)
có \(\sqrt{2020x-2019}+2019\left(x+1\right)-\sqrt{2019x-20120}\)\(=0\)
\(\Leftrightarrow\sqrt{2020x-2019}-\sqrt{2019x-2020}=-2019\left(x+1\right)\)
\(\Leftrightarrow2020x-2019-\left(2019x-2020\right)=-2019\left(x+1\right)\left(\sqrt{2020x-2019}+\sqrt{2019x-2020}\right)\)
\(\Leftrightarrow\left(x+1\right)+2019\left(x+1\right)\left(\sqrt{2020x-2019}+\sqrt{2019x-2020}\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[1+2019\left(\sqrt{2020x-2019}+\sqrt{2019x-2020}\right)\right]=0\)
\(\Leftrightarrow x+1=0\Leftrightarrow x=-1\)(không thỏa mãn)
vậy phương trình vô nghiệm

ĐKXĐ: \(x\ge\dfrac{2020}{2019}>0\)
\(\Leftrightarrow\sqrt{2020x-2019}+\sqrt{2019x-2020}+2019\left(x+1\right)=0\)
\(\Leftrightarrow\dfrac{x+1}{\sqrt{2020x-2019}+\sqrt{2019x-2020}}+2019\left(x+1\right)=0\)
Do \(x>0\) nên hiển nhiên vế trái dương.
Pt vô nghiệm
ĐKXĐ: x≥20202019>0x≥20202019>0
⇔√2020x−2019+√2019x−2020+2019(x+1)=0⇔2020x−2019+2019x−2020+2019(x+1)=0
⇔x+1√2020x−2019+√2019x−2020+2019(x+1)=0⇔x+12020x−2019+2019x−2020+2019(x+1)=0
Do x>0x>0 nên hiển nhiên vế trái dương.
Pt vô nghiệm

Phương trình x + x − 1 = 0 có chứa căn thức bên không là phương trình bậc hai một ẩn.
Phương trình 2x + 2y2 + 3 = 9 có chứa hai biến x; y nên không là phương trình bậc hai một ẩn.
Phương trình 1 x 2 + x + 1 = 0 có chứa ẩn ở mẫu thức nên không là phương trình bậc hai một ẩn.
Phương trình 2 x2 + 1 = 0 và x2 + 2019x = 0 là những phương trình bậc hai một ẩn.
Vậy có hai phương trình bậc hai một ẩn trong số các phương trình đã cho.
Đáp án cần chọn là: A

1) Phương trình ban đầu tương đương :
\(\left(2021x-2020\right)^3=\left(2x-2\right)^3+\left(2019x-2018\right)^3\)
Đặt \(a=2x-2,b=2019x-2018\)
\(\Rightarrow a+b=2021x-2020\)
Khi đó phương trình có dạng :
\(\left(a+b\right)^3=a^3+b^3\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow3\cdot\left(2x-2\right)\cdot\left(2019x-2018\right)\cdot\left(2021x-2002\right)=0\)
\(\Leftrightarrow\)Hoặc \(2x-2=0\)
Hoặc \(2019x-2018=0\)
Hoặc \(2021x-2020=0\)
\(\Rightarrow x\in\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\) (thỏa mãn)
Vậy : phương trình đã cho có tập nghiệm \(S=\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\)
\(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\)
\(\Leftrightarrow2x^2-3x+x^2-xm=3x^2+x-m\)
\(\Leftrightarrow-3x-xm=x-m\)
\(\Leftrightarrow4x+xm=m\Leftrightarrow x\left(4+m\right)=m\)
\(\Leftrightarrow x=\frac{m}{m+4}\)
Phương trình có nghiệm không âm \(\Leftrightarrow x\ge0\)
\(\Rightarrow\frac{m}{m+4}\ge0\)
Mà \(m+4>m\)nên \(\orbr{\begin{cases}m\ge0\\m+4\le0\end{cases}}\Leftrightarrow\orbr{\begin{cases}m\ge0\\m\le-4\end{cases}}\)

Lời giải:
Ta có: $\Delta=(m-3)^2+16>0$ với mọi $m$ nên pt luôn có 2 nghiệm phân biệt $x_1,x_2$ với mọi $m$.
Theo định lý Viet:
$x_1+x_2=m-3$
$x_1x_2=-4$
Có:
$\sqrt{x_1^2+2020}-x_1=\sqrt{x_2^2+2020}+x_2$
$\Leftrightarrow \sqrt{x_1^2+2020}-\sqrt{x_2^2+2020}=x_1+x_2$
$\Leftrightarrow \frac{x_1^2-x_2^2}{\sqrt{x_1^2+2020}+\sqrt{x_2^2+2020}}=x_1+x_2$
$\Leftrightarrow (x_1+x_2)\left[\frac{x_1-x_2}{\sqrt{x_1^2+2020}+\sqrt{x_2^2+2020}}-1\right]=0$
$\Leftrightarrow x_1+x_2=0$ hoặc $x_1-x_2=\sqrt{x_1^2+2020}+\sqrt{x_2^2+2020}$
Với $x_1+x_2=0$
$\Leftrightarrow m-3=0\Leftrightarrow m=3$ (tm)
Với $x_1-x_2=\sqrt{x_1^2+2020}+\sqrt{x_2^2+2020}$
$\Rightarrow (x_1-x_2)^2=(\sqrt{x_1^2+2020}+\sqrt{x_2^2+2020})^2$
$\Leftrightarrow -2x_1x_2=4040+2\sqrt{(x_1^2+2020)(x_2^2+2020)}$
$\Leftrightarrow 8=4040+2\sqrt{(x_1^2+2020)(x_2^2+2020)}$
$\Leftrightarrow \sqrt{(x_1^2+2020)(x_2^2+2020)}=-2016<0$ (vô lý - loại)
Vậy $m=3$
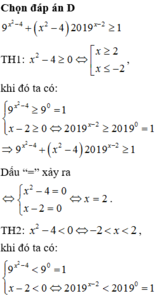

x=2020; x=1
\(x^2+2019x=2020\)
\(x\left(x+2019\right)=2020\)
Tách 2020 ra 2 thừa số có hiệu là 2019: 2020 = 1*2020 = (-1) * (-2020)
Mà thừa số x luôn bé hơn thừa số x + 2019
\(\Rightarrow x\in\left\{1;-2020\right\}\)