làm hộ mk bài này nhé cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HG
hương giang
20 tháng 3 2020
https://i.imgur.com/grd6wG8.jpg
Đúng(0)
Những câu hỏi liên quan
NT
3
MN
19 tháng 1 2022
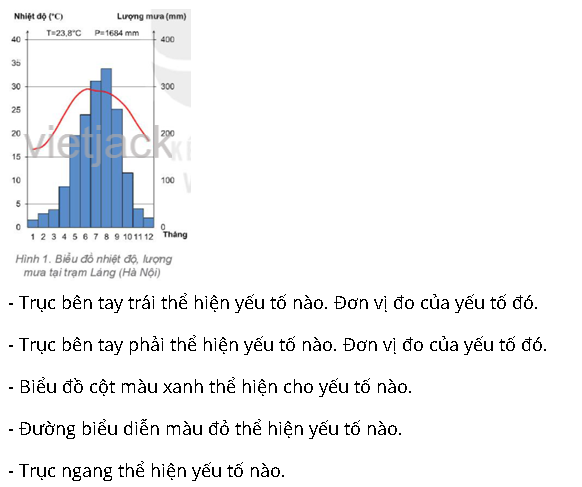
- Trục bên tay trái thể hiện nhiệt độ. Đơn vị đo: °C.
- Trục bên tay phải thể hiện lượng mưa. Đơn vị đo: mm.
- Biểu đồ cột màu xanh thể hiện lượng mưa.
- Đường biểu diễn màu đỏ thể hiện nhiệt độ.
- Trục ngang thể hiện các tháng trong năm.
LL
19 tháng 1 2022
Trục bên tay trái thể hiện yếu tố nhiệt độ. Đơn vị đo là 0C.
- Trục bên tay phải thể hiện yếu tố lượng mưa. Đơn vị đo là mm.
- Biểu đồ cột màu xanh thể hiện cho yếu tố lượng mưa trung bình tháng.
- Đường biểu diễn màu đỏ thể hiện yếu tố nhiệt độ trung bình tháng.
- Trục ngang thể hiện các tháng trong năm.
NM
2
NN
15 tháng 7 2019
( 0,2 + 0,4 + 0,6 + ... + 3,2 ) x ( 4,5 x 3,6 - 8,1 x 2 )
= ( 0,2 + 0,4 + 0,6 + ... + 3,2 ) x ( 16,2 - 16,2 )
= ( 0,2 + 0,4 + 0,6 + ... + 3,2 ) x 0
= 0
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
BC
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
7
AH
Akai Haruma
Giáo viên
17 tháng 2 2021
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
PT
3