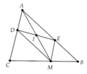
Cho \(\bigtriangleup\text{ABC}\), lấy điểm M bất kì nằm trên cạnh BC. Qua M dựng đường thẳng song song với với AB cắt AC tại D. Qua M dựng đường thẳng song song với AC cắt AB tại E.
a) Chứng minh \(\diamond\text{ADME}\) là hình gì ?
b) Tìm vị trí của điểm M trên cạnh BC để \(\diamond\text{ADME}\) là hình thoi.
c) Tìm điều kiện của \(\bigtriangleup\text{ABC}\) và vị trí của điểm M trên cạnh BC để \(\diamond\text{ADME}\) là hình vuông.
[ Nhớ vẽ hình đẹp, đầy đủ, lời giải rõ ràng sẽ được tick đúng ]

\(\text{GIẢI :}\)
Chứng minh :
a) Xét \(\diamond\text{AEMD}\), có \(\hept{\begin{cases}\text{AE // DM }\\\text{EM // AD}\end{cases}}\)
\(\Rightarrow \text{ }\diamond\text{AEMD}\) là hình bình hành.
b) Để hình bình hành AEMD là hình thoi \(\Rightarrow\) AM là đường phân giác của góc A.
c) Để hình bình hành AEMD là hình vuông \(\Rightarrow\text{ }\hept{\begin{cases}\bigtriangleup\text{ABC vuông tại A}\\\text{AM là đường phân giác góc A}\end{cases}}\).