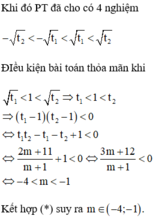Cho hàm số y = x2 - 4.x + 3 có đồ thị (P) . Tìm giá trị để tham số m để đường thẳng ( dm ) : y = x + m cắt đồ thị ( P ) tại 2 điểm phân biệt có hoành độ x1 , x2 thỏa mãn \(\frac{1}{x_1}+\frac{1}{x_2}=2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 12 2020
- Xét phương trình hoành độ giao điểm :
\(x^2-3mx+m^2+1=mx+m^2\)
\(\Leftrightarrow x^2-4mx+1=0\) ( 1 )
Có : \(\Delta^,=4m^2-1\)
- Để (d) cắt ( P ) tại 2 điểm phân biệt trên trục hoành
<=> Phương trình ( 1 ) có 2 nghiệm phân biệt .
<=> \(\Delta^,=4m^2-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{1}{2}\end{matrix}\right.\)
- Theo viets : \(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1x_2=1\end{matrix}\right.\)
( đến đây giải nốt nhá hình như thiếu đề đoạn thỏa mãn :vvv )
24 tháng 1 2022
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=2x-1\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
b: Phương trình hoành độ giao điểm là:
\(x^2-mx+m-1=0\)
\(\text{Δ}=\left(-m\right)^2-4\cdot1\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2>=0\)
Để phương trình có hai nghiệm phân biệt thì m-2<>0
hay m<>2
Theo đề, ta có: \(x_1+x_2+2\sqrt{x_1x_2}=9\)
\(\Leftrightarrow m+2\sqrt{m-1}=9\)
\(\Leftrightarrow\sqrt{m-1}=\dfrac{9-m}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}1< m< 9\\m^2-18m+81-4m+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1< m< 9\\\left(m-5\right)\left(m-17\right)=0\end{matrix}\right.\)
=>m=5
CM
8 tháng 9 2019
Đáp án A
Phương trình hoành độ giao điểm
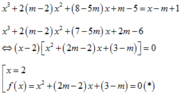
Để phương trình có 3 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 2
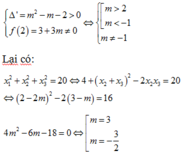
Vậy có 2 giá trị của m thỏa mãn.
27 tháng 4 2023
- Phương trình hoành độ giao điểm của (P) và (d'):
\(-x^2=mx-4\Leftrightarrow x^2+mx-4=0\left(1\right)\)
\(a=1;b=m;c=-4\)
\(\Delta=b^2-4ac=m^2-4.\left(1\right).\left(-4\right)=m^2+16>0\)
Vì \(\Delta>0\) nên (P) và (d) luôn cắt nhau tại hai điểm phân biệt có hoành độ x1, x2.
Theo định lí Viete cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{m}{1}=-m\\x_1x_2=\dfrac{c}{a}=\dfrac{-4}{1}=-4\end{matrix}\right.\)
Ta có: \(\left(x_1-x_2\right)^2-\left(x_1+x_2\right)=18\)
\(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=18\)
\(\Rightarrow\left(-m\right)^2-2.\left(-4\right)-\left(-m\right)-18=0\)
\(\Leftrightarrow m^2+m-12=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)
Vậy m=4 hay m=-3.