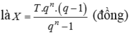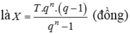ông Mạnh mua chiếc xe với giá 10500000đ. Cửa hàng đề nghị ông trả ngay 1800000đ tiền mặt, 2900000đ cuối 2 năm tiếp theo và 2000000đ cuối các năm thứ 3 và thứ 4. Biết lãi suất áp dụng là 5,85%. Hỏi ông Mạnh sau 4 năm còn nợ bao nhiêu tiền
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C
Do lãi suất theo năm là 8% nên lãi suất tính theo tháng là
![]()
Cuối tháng 1, sau khi trả nợ 2 triệu, ông Bình còn nợ: ![]() triệu đồng.
triệu đồng.
Cuối tháng 2, sau khi trả nợ 2 triệu, ông Bình còn nợ:
![]()
![]() triệu đồng.
triệu đồng.
Cuối tháng 3, sau khi trả nợ 2 triệu, ông Bình còn nợ ![]()
![]()
….
Cuối tháng m, sau khi trả nợ 2 triệu, ông Bình còn nợ 0 đồng, nghĩa là
Ta có ![]() là tổng tất cả các số hạng của một cấp số nhân có
u
1
=
1
và công bội
q
=
n
+
1
gồm m số hạng
là tổng tất cả các số hạng của một cấp số nhân có
u
1
=
1
và công bội
q
=
n
+
1
gồm m số hạng ![]()
![]()

Ta có 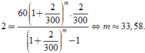
Vậy ông Bình trả hết nợ sau 34 tháng.

Gọi unn là số tiền sau mỗi tháng ông An còn nợ ngân hàng.
Lãi suất mỗi tháng là 1% .
Ta có:
u1 = 1 000 000 000 đồng.
u2 = u1 + u1.1% - a = u1(1 + 1%) – a (đồng)
u3 = u1(1 + 1%) – a + [u1(1 + 1%) – a].1% – a = u1(1 + 1%)2 – a(1 + 1%) – a
...
un = u1(1 + 1%)n-1 – a(1 + 1%)n-2 – a(1 + 1%)n-3 – a(1 + 1%)n-4 – ... – a.
Ta thấy dãy a(1 + 1%)n-1; a(1 + 1%)n-3; a(1 + 1%)n-4; ...; a lập thành một cấp số nhân với số hạng đầu a1 = a và công bội q = 1 + 1% = 99% có tổng n – 2 số hạng đầu là:
\({S_{n - 2}} = \frac{{a\left[ {1 - {{\left( {99\% } \right)}^{n - 2}}} \right]}}{{1 - 99\% }} = 100a\left[ {1 - {{\left( {99\% } \right)}^{n - 2}}} \right]\).
Suy ra un = u1(1 + 1%)n-1 – 100a[1 – (99%)n-2].
Vì sau 2 năm = 24 tháng thì ông An trả xong số tiền nên n = 24 và u24 = 0. Do đó ta có:
u24 = u1(1 + 1%)23 – 100a[1 – (99%)22] = 0
⇔ 1 000 000 000.(99%) – 100a[1 – (99%)22] = 0
⇔ a = 40 006 888,25
Vậy mỗi tháng ông An phải trả 40 006 888,25 đồng.