Cho tam giác ABC vuông tại A. Gọi M,N lần lượt là trung điểmcủa AB,BC.
a) Gọi D là điểm đối xứng của A quaN
Chứng minh: Tứ giác ABCD là HCN
b) Lấy I là trung điểm của AC, E là điểm đối xứng của N qua I. Chứng minh: tứ giác ANCE là hình thoi
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G'. Chứng minh: BG=CG'
d) Cho AB=6 cm, AC=8 cm. Tính Diện tích tam giác DGG'
Ai giúp với !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

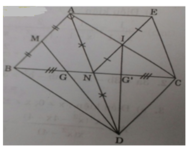
Bạn tự vẽ hình nha :))
a) Xét tứ giác ABCD có :
NB = NC ( N là trung điểm của BC ( gt ))
NA = ND ( D đối xứng với A qua N ( gt ))
BC giao AD tại N
=> Tư giác ABCD là hình bình hành ( dhnb )
mà \(\widehat{BAC}=90^0\) ( \(\Delta ABC\)vuông tại A (gt))
=> Tứ giác ABCD là HCN ( dhnb )
b) Xét tam giác ABC có :
N là trung điểm của BC ( gt )
I là trung điểm của AC ( gt )
=> NI là đường trung bình của tam giác ABC ( đ/n )
=> NI // AB ( t/c )
=> \(\widehat{BAC}=\widehat{NIC}=90^0\) ( đồng vị )
=> NI \(\perp\)AC
Xét tứ giác ANCE có :
IA = IC ( I là trung điểm của AC (gt))
IN = IE ( E đối xứng N qua I (gt))
AC giao NE tại I
=> Tứ giác ANCE là hình bình hành ( dhnb )
mà NI \(\perp\)AC ( cmt )
=> Tứ giác ANCE là hình thoi ( dhnb )
c) Xét tam giác ABD có :
DM là đường trung tuyến
BN là đường trung tuyến
DM giao BN tại G
=> G là trọng tâm.
\(\Rightarrow BG=\frac{2}{3}BN\) mà \(BN=\frac{1}{2}BC\) ( ABCD là HCN (a))
\(\Rightarrow BG=\frac{1}{3}BC\)
CM tương tự, ta có : \(CH=\frac{1}{3}BC\)
\(\Rightarrow BG=CH\left(=\frac{1}{3}BC\right)\)
Thanks