Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
M là trung điểm của AB
P là trung điểm của BC
Do đó: MP là đường trung bình của ΔBAC
Suy ra: MP//AC và \(MP=\dfrac{AC}{2}=5\left(cm\right)\)
Xét ΔABC có
N là trung điểm của AC
P là trung điểm của BC
Do đó: NP là đường trung bình của ΔABC
Suy ra: NP//AB và \(NP=\dfrac{AB}{2}=2.5\left(cm\right)\)
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}=5\left(cm\right)\)

a: Xét tứ giác APCQ có
N là trung điểm của AC
N là trung điểm của PQ
Do đó: APCQ là hình bình hành
Suy ra: AQ//PC
hay AQ//BC(1)
Xét tứ giác AEBP có
M là trung điểm của AB
M là trung điểm của PE
Do đó: AEBP là hình bình hành
Suy ra: AE//BP
hay AE//BC(2)
Từ (1) và (2) suy ra E,A,Q thẳng hàng

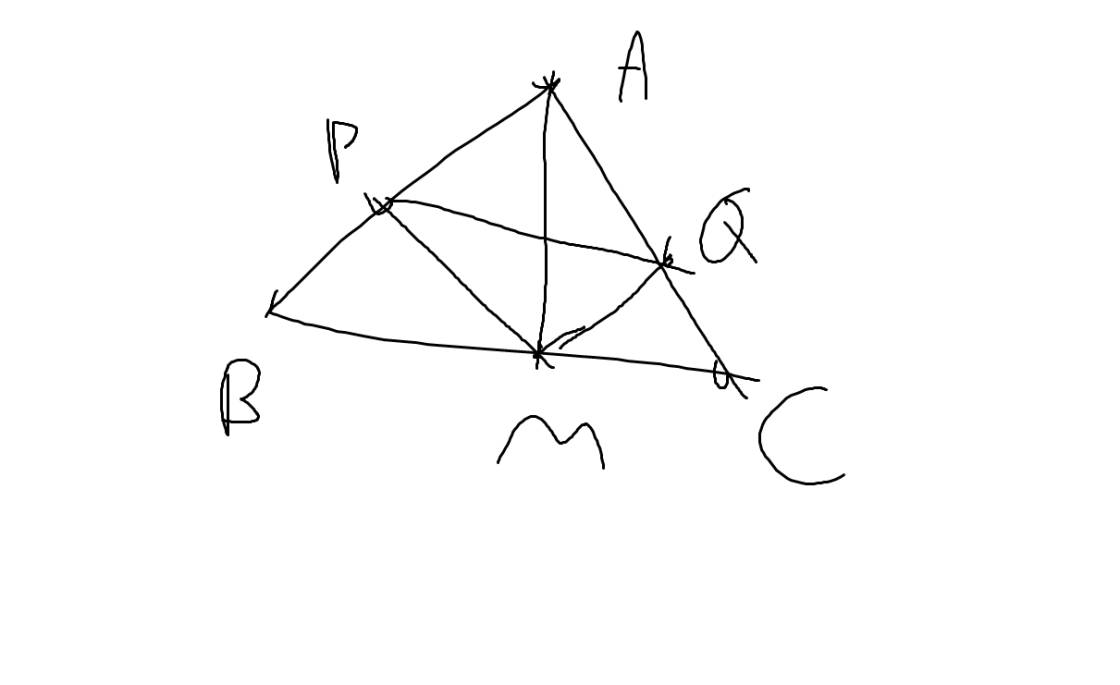
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ

a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC hay MN//BP và \(MN=\dfrac{1}{2}BC=BP\)
Vậy BMNP là hbh
b, Vì BMNP là hbh mà I là trung điểm MP nên I là trung điểm BN
Vậy B,I,N thẳng hàng

a: Xét ΔABC có
AM/AB=AN/AC
Do đó: MN//BC
hay BMNC là hình thang
mà BN=CM
nên BMNC là hình thang cân

\(c,\) Vì AD//BP và AD=BP nên ADPB là hbh
Do đó O là trung điểm AP và BD
Xét tam giác ADP có DO và AN là trung tuyến giao tại G nên G là trọng tâm
Do đó \(DG=\dfrac{2}{3}DO\)
Mà \(DO=\dfrac{1}{2}BD\Rightarrow DG=\dfrac{2}{3}\cdot\dfrac{1}{2}BD=\dfrac{1}{3}BD\)

a, Vì N,P là trung điểm AB,BC nên NP là đtb tg ABC
Do đó NP//AB hay PQ//AM nên MAQP là hình thang
Và \(NP=\dfrac{1}{2}AB=AM\) (M là trung điểm AB)
Mà NP//AB nên NP//AM
Vậy MANP là hbh
NP là đường trung bình của tg ABC \(\Rightarrow NP=\frac{AB}{2}=AM\)
\(\Rightarrow MP+NP=MP+AM\)
Xét tg AMP có
\(MP+AM>AP\) (Trong tg tổng 2 cạnh lớn hơn cạnh còn lại)
=> Bạn xem lại đề bài