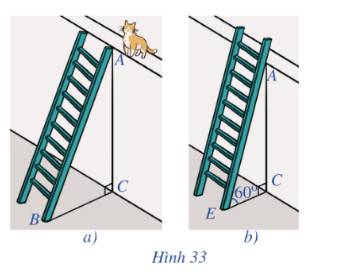
Gần nhà bạn Thu có một bức tường rào xung quanh nhà. Để trèo lên bức tường bạn Thu đã dùng một chiếc thang đặt gần bức tường. Biết rằng chiều dài của thang là 5 m và chân thang cách tường là 3 m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


( Hình ảnh chỉ có tính chất minh họa )
Áp dụng định lý Pytago vào tam giác ABC, ta có:
AB2 + AC2 = BC2
=> AB2 + 32 = 52
=> AB2 + 9 = 25
=> AB2 = 25 - 9
=> AB2 = 16
=> AB = 4m
nhớ tk cho mk nha
bạn bị hâm à?đến bạn còn trả biết làm mà bạn đi bảo mình làm là sao? hỏi bạn khác đi.

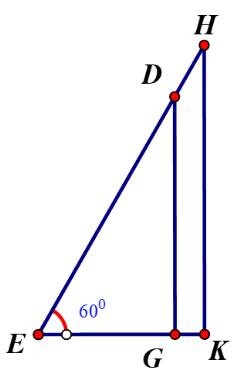
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.

35dm=3,5m
Chiều cao của bức tường là:
\(\sqrt{3.5^2-0.8^2}\simeq3,41\left(m\right)\)

Gọi độ dài của thang là BC, khoảng cách từ chân thang đến chân tường là AC
Theo đề, ta có: BC=3,5m; AC=1,6m; AC\(\perp\)AB tại A
Ta có: ΔABC vuông tại A
=>\(cosC=\dfrac{CA}{CB}\)
=>\(cosC=\dfrac{1.6}{3.5}=\dfrac{16}{35}\)
=>\(\widehat{C}\simeq63^0\)
=>\(60^0< =\widehat{C}< =65^0\)
=>Đạt tiêu chuẩn
CÂU HỎI LÀ GÌ THẾ????????
Hãy tính chiều cao của bức tường đó.