Cho hình vuông ABCD có H và K lần lượt là trung điểm của các cạnh AB và AD. Trên đường thẳng vuông góc với (ABCD) tại H lấy điểm S khác H.
Chứng minh: CK vuông góc với SD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2023
tham khảo:
a) Tam giác ABD có HK là đường trung bình nên HK//BD
Vì ABCD là hình vuông nên AC⊥BD. Suy ra AC⊥HK
Vì SH⊥(ABCD) nên SH⊥AC
Ta có: AC⊥SH,AC⊥HK nên AC⊥(SHK)
b) Ta có tam giác AHD và tam giác DKC bằng nhau nên DH⊥CK
Mà SH⊥(ABCD) nên SH⊥CK
Suy ra CK⊥(SDH)
25 tháng 10 2023
a: Xét tứ giác ABCD có
O là trung điểm chung của AC và BD
=>ABCD là hình bình hành
b: Xét ΔOHA vuông tại H và ΔOKC vuông tại K có
OA=OC
\(\widehat{AOH}=\widehat{COK}\)
Do đó: ΔOHA=ΔOKC
=>OH=OK
=>O là trung điểm của HK
CM
2 tháng 4 2019
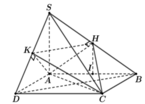
Tham khảo hình vẽ. Ta sẽ sử dụng công thức 
Đặt SA = x (x > 0) Tính được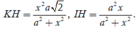 
Chứng minh được 
Khi đó 
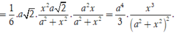
Xét hàm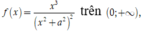 
ta có 
Suy ra thể tích khối tứ diện lớn nhất bằng 
Chọn C.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) Ta có:
\(SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot CB\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AB \bot CB\)
\( \Rightarrow CB \bot \left( {SAB} \right)\)
\(SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot CD\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AD \bot CD\)
\( \Rightarrow CD \bot \left( {SAD} \right)\)
b) Ta có:
\(\left. \begin{array}{l}CB \bot \left( {SAB} \right) \Rightarrow CB \bot AH\\AH \bot SB\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)
\(\left. \begin{array}{l}CD \bot \left( {SAD} \right) \Rightarrow CD \bot AK\\AK \bot SD\end{array} \right\} \Rightarrow AK \bot \left( {SC{\rm{D}}} \right) \Rightarrow AK \bot SC\)
\( \Rightarrow SC \bot \left( {AHK} \right) \Rightarrow SC \bot HK\)
\(\begin{array}{l}\Delta SAB = \Delta SA{\rm{D}}\left( {c.g.c} \right) \Rightarrow SH = SK,SB = S{\rm{D}}\\\left. \begin{array}{l} \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{S{\rm{D}}}} \Rightarrow HK\parallel B{\rm{D}}\\SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot B{\rm{D}}\end{array} \right\} \Rightarrow SA \bot HK\end{array}\)
\(\left. \begin{array}{l}SC \bot HK\\SA \bot HK\end{array} \right\} \Rightarrow HK \bot \left( {SAC} \right) \Rightarrow HK \bot AI\)