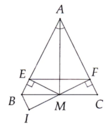
Bài 1: cho tam giác DEF cân tại D.Gọi M là trung trực của EF
a) chứng minh DM vuông góc EF
b) qua F, kẻ đường thẳng song song với DE, cắt tia dm tại K. chứng minh tam giác DFK cân
c) tính chu vi tam giác DFK, biết DE:EF = 2:3 và EF+ 2DE=14
d) trên cạnh DE lấy điểm A,trên cạnh KF lấy điểm B sao cho DA=KB. chứng minh: 3 điểm A,M,B thẳng hàng
Bài 2: cho tam giác MNP cân tại M. kẻ MK vuông góc PN ( K thuộc NP)
a) chứng minh tam giác MNK= tam giác MPK và MK là đường trung trực của đoạn thẳng NP
b) trên tia đối của tia NP lấy điểm A, trên tia đối của tia PN lấy điểm B sao cho AN = BP. chứng minh MA=MB
c) lấy D là một điểm bất kì trên cạnh MA ( D khác A,M) .qua D, kẻ đường thẳng song song với AB, cắt MB tại E. chứng minh tam giác MDE cân
d) chứng minh 3 đường thẳng ND, MK,PE cùng đi qua 1 điểm