Cho a, b, c không âm và a+b+c=3. Tìm GTLN của P = ab2+bc2+ca2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A.
Gọi A(a;0;0); B(0;b;0); C(0;0;c) (a; b; c > 0)
→ Phương trình mặt phẳng (P) là

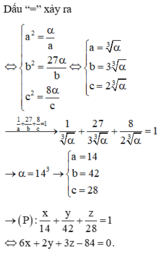
* PS: do a; b; c > 0 nên chỉ có đáp án A thỏa mãn.

Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900

a,b,c \(\ge\)0 và a + b + c =3 \(\Rightarrow a,b,c< 4\)
giả sử b là số nằm giữa a,c thì ( b - a ) ( b - c ) \(\le\)0
\(\Leftrightarrow b^2+ac\le ab+bc\Rightarrow ab^2+a^2c\le abc+a^2b\)
\(\Rightarrow ab^2+bc^2+ca^2\le abc+a^2b+bc^2\le a^2b+bc^2+2abc=b\left(a+c\right)^2=b\left(3-b\right)^2\)
Cần chứng minh \(b\left(3-b\right)^2\le4\Leftrightarrow b^3-6b^2+9b-4\le0\Leftrightarrow\left(b-1\right)^2\left(b-4\right)\le0\)( luôn đúng )
Vậy GTLN của P là 4 khi ( a,b,c ) là hoán vị của bộ số ( 0 ; 1 ; 2 )

Tìm GTNN của P=a^7+b^7+c^7 biết a^3b^3+b^3c^3+c^3a^3>=1 - Sasu ka

Ta có:
\(\frac{\left(a+b+c\right)^2}{3}\le a^2+b^2+c^2=2\left(a+b+c\right)\)
=> \(\left(a+b+c\right)^2-6\left(a+b+c\right)\le0\)
=> \(0\le a+b+c\le6.\)
\(T=\frac{a}{a+1}+\frac{b}{b+a}+\frac{c}{c+1}=1-\frac{1}{a+1}+1-\frac{1}{b+1}+1-\frac{1}{c+1}\)
\(=3-\left(\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}\right)\le3-\frac{\left(1+1+1\right)^2}{a+b+c+3}\le3-\frac{3^2}{6+3}=2\)
"=" xảy ra <=> \(a=b=c\)và \(a+b+c=6\)<=> \(a=b=c=2\)
Vậy max T = 2 khi và chỉ khi a=b=c =2


Lời giải:
Giả sử \(b=\text{mid}(a,b,c)\Rightarrow (b-a)(b-c)\leq 0\)
\(\Leftrightarrow b^2+ac\leq bc+ba\)
\(\Rightarrow b^2a+a^2c\leq abc+a^2b\)
\(\Rightarrow ab^2+bc^2+ca^2\leq abc+a^2b+bc^2\)
Lại có, áp dụng BĐT AM-GM:
\(abc+a^2b+bc^2=b(ac+a^2+c^2)\leq b(2ac+a^2+c^2)=b(a+c)^2=\frac{1}{2}.2b(a+c)(a+c)\)
\(\leq \frac{1}{2}\left(\frac{2b+a+c+a+c}{3}\right)^3=\frac{1}{2}\left(\frac{2(a+b+c)}{3}\right)^3=4\)
Vậy $P_{\max}=4$ khi $(a,b,c)=(2,1,0)$ và hoán vị.