Tìm nguyên hàm của hàm số f(x)=2x−1/√1−x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 2 2019
Chọn D
Đặt t = 2 x + 1 ⇒ d t = 1 2 x + 1 d x ⇒ d x = t d t
⇒ ∫ 2 x + 1 d x = ∫ t 2 d t = t 3 3 + C = 1 3 2 x + 1 2 x + 1 + C
PT
1
LT
1
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
\(\int f(x)dx=\int \frac{x^2+2x}{x+1}dx=\int \frac{(x+1)^2-1}{x+1}dx=\int (x+1-\frac{1}{x+1})dx\)
\(=\int (x+1)dx-\int \frac{1}{x+1}dx=\frac{x^2}{2}+x-\ln |x+1|+c\)
CM
17 tháng 6 2019
Chọn A
∫ 2 x 2 + 2 x + 3 2 x + 1 d x = ∫ 2 x + 1 2 + 5 2 2 x + 1 d x = 1 8 ( 2 x + 1 ) 2 + 5 4 ln 2 x + 1 + C
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
2.
\(I=\int e^{3x}.3^xdx\)
Đặt \(\left\{{}\begin{matrix}u=3^x\\dv=e^{3x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=3^xln3dx\\v=\dfrac{1}{3}e^{3x}\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}\int e^{3x}.3^xdx=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}.I\)
\(\Rightarrow\left(1+\dfrac{ln3}{3}\right)I=\dfrac{1}{3}e^{3x}.3^x\)
\(\Rightarrow I=\dfrac{1}{3+ln3}.e^{3x}.3^x+C\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
1.
\(I=\int\left(2x-1\right)e^{\dfrac{1}{x}}dx=\int2x.e^{\dfrac{1}{x}}dx-\int e^{\dfrac{1}{x}}dx\)
Xét \(J=\int2x.e^{\dfrac{1}{x}}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{\dfrac{1}{x}}\\dv=2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\dfrac{e^{\dfrac{1}{x}}}{x^2}dx\\v=x^2\end{matrix}\right.\)
\(\Rightarrow J=x^2.e^{\dfrac{1}{x}}+\int e^{\dfrac{1}{x}}dx\)
\(\Rightarrow I=x^2.e^{\dfrac{1}{x}}+C\)
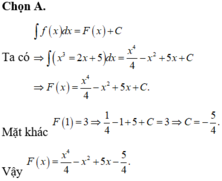
Đặt \(\sqrt{1-x}=t\Rightarrow x=1-t^2\Rightarrow dx=-2tdt\)
\(I=\int\frac{2\left(1-t^2\right)-1}{t}\left(-2tdt\right)=\int\left(4t^2-2\right)dt=\frac{4}{3}t^3-2t+C\)
\(=\frac{4}{3}\left(1-x\right)\sqrt{1-x}-2\sqrt{1-x}+C\)