Giá trị của x để 4-12x không âm là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HS
18 tháng 5 2018
Để \(M=5xy^3+4x^2y^2-12x^3y\\ \) và \(A=x\left(x^3+12x^2y-5y^3\right)\) ko âm
\(\Rightarrow\)\(M+A\)cũng đồng thời >0
\(\Rightarrow\)\(M+A=\left(5xy^3+4x^2y^2-12x^3y\right)+\left(x^4+12x^3y-5y^3x\right)\)
\(\Rightarrow\)\(M+A=\left(5xy^3-5xy^3\right)-\left(12x^3y-12x^{3y}\right)+\left(x^4+4x^2y^2\right)\)
\(\Rightarrow M+A=x^4+4x^2y^2\)
Mà \(x^4\ge0\) \(;4x^2y^2\ge0\)
\(\Rightarrow\)\(x^4+4x^2y^2\ge0\)
\(\Rightarrow\)\(M+A\ge0\)
20 tháng 9 2021
a: ta có: \(A=x^2-3x+10\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{31}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}>0\forall x\)
b: Ta có: \(B=x^2-5x+2021\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{8015}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{8015}{4}>0\forall x\)
5 tháng 11 2017
Q = x^2-12x+36+5
= x^2 - 2.x.6 + 6^2 + 5 = (x-6)^2 + 5 >=5 với mọi x
=> Q luôn ko âm với mọi giá tri biến ( ĐPCM )
5 tháng 11 2017
Ta có: Q = x^2 - 12x + 41
= x^2 - 2.x.6 + 62 + 5
= (x-6)2 + 5
Vì bình phương 1 số luôn dương và 5>0 nên Q >0
LV
1
7 tháng 7 2020
\(\frac{5}{4-x}\left(đkxđ:x\ne4\right)\)
Phân số không âm khi cả tử và mẫu hoặc cùng dương hoặc cùng âm
5 là số dương
=> Để \(\frac{5}{4-x}\)không âm => 4 - x dương
=> 4 - x > 0
=> -x > -4
=> x < 4
Vậy với x < 4 thì \(\frac{5}{4-x}\)không âm
CM
21 tháng 11 2017
Chọn D.
Tam thức bậc hai f(x) = x 2 - 12x - 13 nhận giá trị không âm khi và chỉ khi
f(x) ≥ 0 ⇔
x
2
- 12x - 13 ≥ 0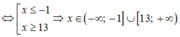 
CM
22 tháng 2 2019
12 − 4x 9 ≥ 0
Û 12 - 4x ≥ 0
Û 4x ≤ 12
Û x ≤ 3
Đáp án cần chọn là: C
Xét biểu thức 4-12x. Để 4-12x không âm thì \(4\ge12x\)
\(\Leftrightarrow x\le\frac{1}{3}\)