Tích: 2x 12x 22x ....x 152x 162
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2023
a: \(=\dfrac{6x^2+9x+8x+12}{2x+3}=\dfrac{3x\left(2x+3\right)+4\left(2x+3\right)}{2x+3}\)
=3x+4
b: \(=\dfrac{5x^2-2x+15x-6}{5x-2}\)
\(=\dfrac{x\left(5x-2\right)+3\left(5x-2\right)}{5x-2}=x+3\)
c: \(=\dfrac{-8x^2+20x+2x-5-10}{2x-5}=-4x+1+\dfrac{-10}{2x-5}\)
d: \(=\dfrac{14x^2-35x+2x-5}{2x-5}=\dfrac{7x\left(2x-5\right)+\left(2x-5\right)}{2x-5}\)
=7x+1
e: \(=\dfrac{2x^3+x^2+6x^2+3x+12x+6}{2x+1}\)
\(=\dfrac{x^2\left(2x+1\right)+3x\left(2x+1\right)+6\left(2x+1\right)}{2x+1}=x^2+3x+6\)
f: \(=\dfrac{x^3-2x^2+6x^2-12x+x-2}{x-2}=x^2+6x+1\)
g: \(=\dfrac{12x^3+6x^2-4x^2-2x+6x+3}{2x+1}=6x^2-2x+3\)
HV
27 tháng 7 2023
chuyển vế sang r phân tích thành nhân tử, có thể dùng máy tính bỏ túi nhé bạn
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 7 2023
câu 1: 9\(x^2\) + 12\(x\) + 5 =11
(3\(x\))2 + 2.3.\(x\) .2 + 22 + 1 = 11
(3\(x\) + 2)2 = 11 - 1
(3\(x\) + 2)2 = 10
\(\left[{}\begin{matrix}3x+2=\sqrt{10}\\3x+2=-\sqrt{10}\end{matrix}\right.\)
\(\left[{}\begin{matrix}3x=\sqrt{10}-2\\3x=-\sqrt{10}-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\sqrt{10}-2}{3}\\x=\dfrac{-\sqrt{10}-2}{3}\end{matrix}\right.\)
Vậy S = {\(\dfrac{-\sqrt{10}-2}{3}\); \(\dfrac{\sqrt{10}-2}{3}\)}
Câu 2: 6\(x^2\) + 16\(x\) + 12 = 2\(x^2\)
6\(x^2\) + 16\(x\) + 12 - 2\(x^2\) = 0
4\(x^2\) + 16\(x\) + 12 = 0
(2\(x\))2 + 2.2.\(x\).4 + 16 - 4 = 0
(2\(x\) + 4)2 = 4
\(\left[{}\begin{matrix}2x+4=2\\2x+4=-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=-2\\2x=-6\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)
S = { -3; -1}
3, 16\(x^2\) + 22\(x\) + 11 = 6\(x\) + 5
16\(x^2\) + 22\(x\) - 6\(x\) + 11 - 5 = 0
16\(x^2\) + 16\(x\) + 6 = 0
(4\(x\))2 + 2.4.\(x\) . 2 + 22 + 2 = 0
(4\(x\) + 2)2 + 2 = 0 (1)
Vì (4\(x\)+ 2)2 ≥ 0 ∀ ⇒ (4\(x\) + 2)2 + 2 > 0 ∀ \(x\) vậy (1) Vô nghiệm
S = \(\varnothing\)
Câu 4. 12\(x^2\) + 20\(x\) + 10 = 3\(x^2\) - 4\(x\)
12\(x^2\) + 20\(x\) + 10 - 3\(x^2\) + 4\(x\) = 0
9\(x^2\) + 24\(x\) + 10 = 0
(3\(x\))2 + 2.3.\(x\).4 + 16 - 6 = 0
(3\(x\) + 4)2 = 6
\(\left[{}\begin{matrix}3x+4=\sqrt{6}\\3x+4=-\sqrt{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}3x=-4+\sqrt{6}\\3x=-4-\sqrt{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}-4}{3}\\x=-\dfrac{\sqrt{6}+4}{3}\end{matrix}\right.\)
S = {\(\dfrac{-\sqrt{6}-4}{3}\); \(\dfrac{\sqrt{6}-4}{3}\)}
NH
1
12 tháng 5 2020
Bài 1:
a) Ta có: 22x-13=x-6
\(\Leftrightarrow22x-13-x+6=0\)
\(\Leftrightarrow21x-7=0\)
\(\Leftrightarrow21x=7\)
hay \(x=\frac{1}{3}\)
Vậy: \(x=\frac{1}{3}\)
b) Ta có: (x-7)(2x+10)=0
\(\Leftrightarrow\left(x-7\right)\cdot2\cdot\left(x+5\right)=0\)
mà \(2\ne0\)
nên \(\left[{}\begin{matrix}x-7=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)
Vậy: \(x\in\left\{-5;7\right\}\)
c) ĐKXĐ: \(x\ne14\)
Ta có: \(\frac{12x+9}{x-14}=7\)
\(\Leftrightarrow12x+9=7\left(x-14\right)\)
\(\Leftrightarrow12x+9=7x-98\)
\(\Leftrightarrow12x+9-7x+98=0\)
\(\Leftrightarrow5x+107=0\)
\(\Leftrightarrow5x=-107\)
hay \(x=\frac{-107}{5}\)(tm)
Vậy: \(x=\frac{-107}{5}\)
d) Ta có: \(\frac{x+2}{4}+\frac{3x-4}{6}=\frac{x-14}{24}\)
\(\Leftrightarrow\frac{6\left(x+2\right)}{24}+\frac{4\left(3x-4\right)}{24}=\frac{x-14}{24}\)
Suy ra: \(6\left(x+2\right)+4\left(3x-4\right)=x-14\)
\(\Leftrightarrow6x+12+12x-16-x+14=0\)
\(\Leftrightarrow17x+10=0\)
\(\Leftrightarrow17x=-10\)
hay \(x=\frac{-10}{17}\)
Vậy: \(x=\frac{-10}{17}\)
CM
16 tháng 7 2017
Chọn A.
Phương pháp: Tính tích phân từ đó tìm a, b, c.
Cách giải: Ta tính
VA
2
LN
12 tháng 8 2018
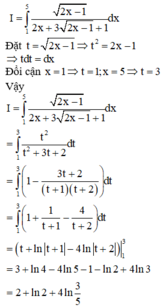
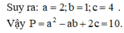
xin lỗi nhé mình mới có lớp 6 à nên ko bít
tha lỗi cho mình nhé!
12 tháng 8 2018
\(\left(x^2+22x-120\right)\left(x^2+33x+270\right)-2x^2\)
\(=x^4+55x^3+876x^2+1980x-32400-2x^2\)
\(=x^4+55x^3+874x^2+1980x-32400\)
22 x 24 + 75 x 22 + 22/22 x 22 - 12 x 22
Lớp 4