\(C=\left|x-500\right|+\left|x-300\right|\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left|500-x\right|+\left|x-300\right|\ge\left|500-x+x-300\right|=200.\)
A min = 200 khi \(300\le x\le500.\)

bai 1 :Ta co |x-3,5| >hoac=0
va |y-1,3| >hoac=0 nen |x-3,5|+|y-1,3|=0 <=> x-3,5=0 va y-1,3=0
=>x=-3,5 va y=-1,3
bai 2: ta co
A=|x-500| +|x-300| =|x-500|+|300-x|
=>A > hoac =|x-500+300-x|=|-200|=200
dau = xay ra<=>(x-500).(300-x)=0 =>300< hoac=x< hoac =500
Bài 1 :
Ta có : \(\left|x-3,5\right|\ge0\) với mọi x
\(\left|y-1,3\right|\ge0\) với mọi x
\(\Rightarrow\left|x-3,5\right|+\left|y-1,3\right|\ge0\) với mọi x
Mà \(\left|x-3,5\right|+\left|y-1,3\right|=0\)
\(\Rightarrow\hept{\begin{cases}\left|x-3,5\right|=0\\\left|y-1,3\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x-3,5=0\\y-1,3=0\end{cases}}\Rightarrow\hept{\begin{cases}x=3,5\\y=1,3\end{cases}}\)
Bài 2 :
Ta có : \(\left|x-500\right|\ge0\) với mọi x
\(\left|x-300\right|\ge0\) với mọi x
\(\Rightarrow\left|x-500\right|+\left|x-300\right|\ge0\) với mọi x
Câu này mk ko bít, làm tới đây đc thôi à

Ta có: \(\left\{{}\begin{matrix}\left|x-500\right|=\left|500-x\right|\ge500-x\\\left|x-300\right|\ge x-300\end{matrix}\right.\)
\(\Rightarrow\left|x-500\right|+\left|x-300\right|\ge\left(500-x\right)+\left(x-300\right)\)
\(\Rightarrow A\ge500-x+x-300=500-300\)
\(\Rightarrow A\ge200\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}\left|500-x\right|=500-x\\\left|x-300\right|=x-300\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}500-x\ge0\\x-300\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le500\\x\ge300\end{matrix}\right.\)
\(\Leftrightarrow300\le x\le500\)
Vậy Min A = 200 \(\Leftrightarrow300\le x\le500\)
Ta có: A = | x - 500 | + | x - 300 |
A = | x - 500 | + | 300 - x |
Áp dụng: | x | + | y | \(\ge\) | x + y |
\(\Rightarrow A\ge\) | x - 500 + 300 - x | = | -200 | = 200
Vậy giá trị của A là 500
A đạt được GTNN \(\Leftrightarrow\) ( x - 500 ) ( 300 - x ) \(\ge\) 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x-500\ge0\\300-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-500< 0\\300-x< 0\end{matrix}\right.\\\\\end{matrix}\right.\) \(\Rightarrow\) \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge500\\x\le300\end{matrix}\right.\\\left\{{}\begin{matrix}x>500\\x>300\end{matrix}\right.\\\\\end{matrix}\right.\)
\(\Rightarrow\) x = 500
Vậy ..........
Chúc bạn hok tốt!!!Nguyen Thi Tra My

3 ) \(A=5+\left|\frac{1}{3}-x\right|\)
Ta có : \(\left|\frac{1}{3}-x\right|\ge0\)
\(\Rightarrow5+\left|\frac{1}{3}-x\right|\ge5\)
Dấu " = " xảy ra khi và chỉ khi \(\frac{1}{3}-x=0\)
\(\Leftrightarrow x=\frac{1}{3}\)
Vậy \(Min_A=5\) khi và chỉ khi \(x=\frac{1}{3}\)
\(B=2-\left|x+\frac{2}{3}\right|\)
Ta có : \(\left|x+\frac{2}{3}\right|\ge0\)
\(\Rightarrow2-\left|x+\frac{2}{3}\right|\ge2\)
Dấu " = " xảy ra khi và chỉ khi \(x+\frac{2}{3}=0\)
\(x=-\frac{2}{3}\)
Vậy \(Min_B=2\) khi và chỉ khi \(x=-\frac{2}{3}\)
c, Vì \(\left\{{}\begin{matrix}\left|x-5,4\right|\ge0\\\left|2,6-x\right|\ge0\end{matrix}\right.\) với mọi x
=>\(\left|x-5,4\right|+\left|2,6-x\right|\ge0\) với mọi x
Do đó \(\left|x-5,4\right|+\left|2,6-x\right|=0\) khi và chỉ khi \(\left\{{}\begin{matrix}\left|x-5,4\right|=0\\\left|2,6-x\right|=0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=5,4\\x=2,6\end{matrix}\right.\)(vô lí)
Vậy không tồn tại x thỏa mãn đề bài.
3,c,
\(C=\left|x-500\right|+\left|x-300\right|=\left|x-500\right|+\left|300-x\right|\ge\left|x-500+300-x\right|=\left|-200\right|=200.\)
Dấu "=" xảy ra khi và chỉ khi \(\left(x-500\right)\left(300-x\right)\ge0\)
<=>\(\left(x-500\right)\left(x-300\right)\le0\)
<=>\(300\le x\le500\).

Lời giải:
$(x^2-x+1)+(x^2-2x+3)+(x^2-3x+5)+....+(x^2-100x+199)=300$
$\Leftrightarrow (x^2+x^2+...+x^2)-(x+2x+3x+...+100x)+(1+3+5+...+199)=300$
$\Leftrightarrow 100x^2-5050x+10000=300$
$\Leftrightarrow 2x^2-101x+200=6$
$\Leftrightarrow 2x^2-101x+194=0$
$\Leftrightarrow (2x-97)(x-2)=0$
$\Rightarrow x=\frac{97}{2}$ hoặc $x=2$

\(\left(5x-1\right)^2-\left(5x-4\right)\left(5x+4\right)=7\)
\(25x^2-10x+1-25x^2+16=7\)
\(17-10x=7\)
\(10x=10\)
\(x=1\)

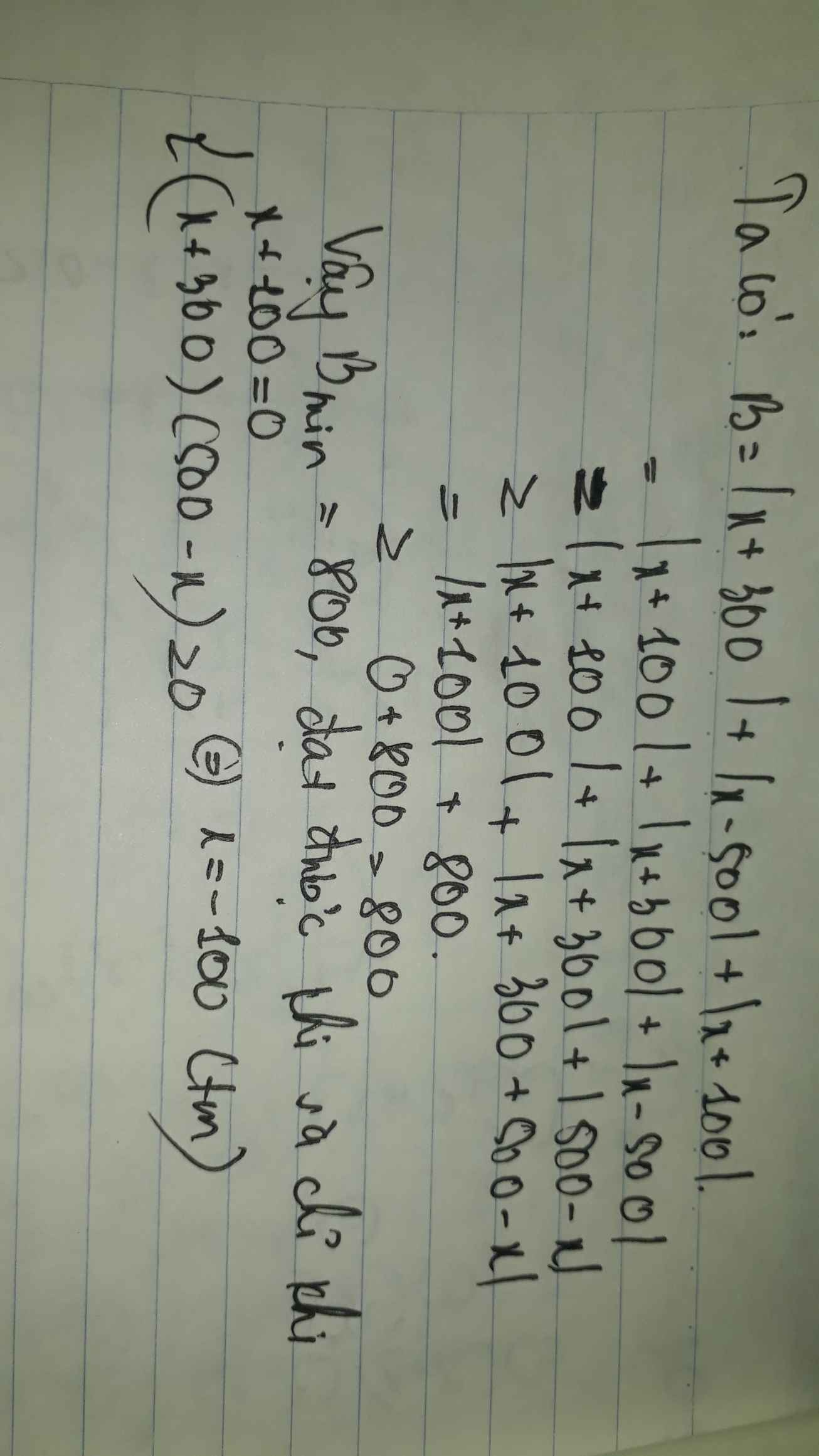
Câu hỏi là gì? Tìm min C à? min C=200 tại \(300\le x\le500\)
Đề bài là tìm giá trị nhỏ nhất hả bạn!
Ta có: \(x=\frac{a}{b},y=\frac{c}{d}\left(a,b,c\in Z;b,d\ne0\right)\)
\(\left|\frac{a}{b}+\frac{c}{d}\right|=\left|\frac{ad+cd}{bd}\right|=\frac{\left|ad+cb\right|}{\left|bd\right|}\left(1\right)\)
Với \(a,b,c,d\)là những số nguyên ta luôn có:
\(\left|ad+cb\right|\le\left|ad\right|+\left|cb\right|\)
\(\Rightarrow\frac{\left|ad\right|}{\left|bd\right|}+\frac{\left|cb\right|}{\left|bd\right|}=\left|\frac{a}{b}\right|+\left|\frac{c}{d}\right|=\left|x\right|+\left|y\right|\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\Rightarrow\left|x+y\right|\le\left|x\right|+\left|y\right|\)
Áp dụng tính chất trên ta có:
\(C=\left|x-500\right|+\left|x-300\right|\ge\left|x-500+x-300\right|\)
Ta có:
\(\left|x-500+x-300\right|=0\)
\(\Rightarrow x-500+x-300=0\)
\(\Rightarrow x+x-500-300=0\)
\(\Rightarrow x+x-\left(500+300\right)=0\)
\(\Rightarrow x+x-800=0\)
\(\Rightarrow x+x=800\)
\(\Leftrightarrow x=400\)
Vậy giá trị nhỏ nhất của C là 0 đạt được khi \(x=400\)