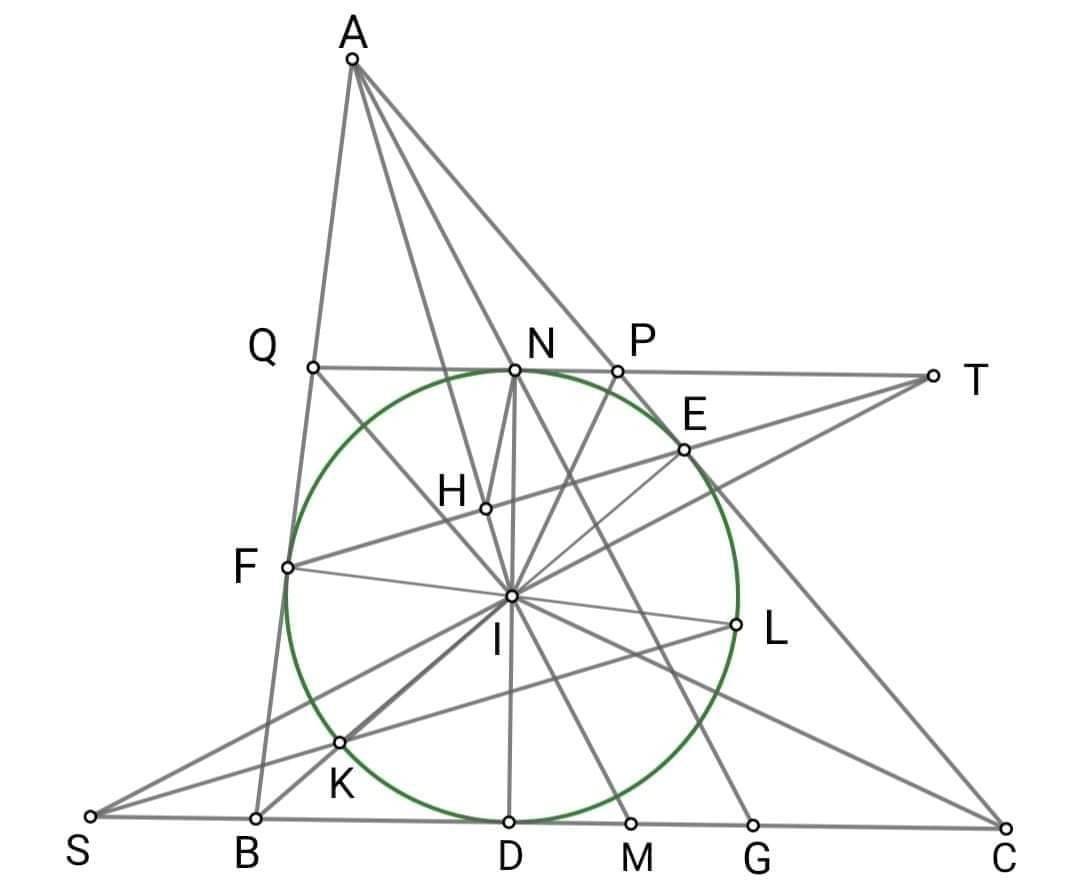
cho tam giác abc đường thẳng d song song bc. Đường thẳng d cắt AB, AC lần lượt tại M,N. Chứng minh (AMN) và (ABC) tiếp xúc nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


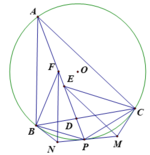
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.

Ta có:
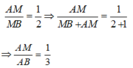
Vì MN// BC nên theo hệ quả định lí Ta let ta có:
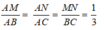
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
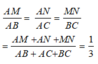
Do đó, tỉ số chu vi tam giác AMN và ABC là 1 3
Chọn đáp án A


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

a) Xét ΔAMN và ΔCND có
\(\widehat{MAN}=\widehat{NCD}\)(hai góc so le trong, AB//CD)
AN=NC(N là trung điểm của AC)
\(\widehat{ANM}=\widehat{CND}\)(hai góc đối đỉnh)
Do đó: ΔAMN=ΔCND(g-c-g)
b) Xét ΔABC có
M là trung điểm của BA(gt)
N là trung điểm của AC(Gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra:MN//BC

a) Xét ΔAMN và ΔCND có
\(\widehat{MAN}=\widehat{NCD}\)(hai góc so le trong, AB//CD)
AN=NC(N là trung điểm của AC)
\(\widehat{ANM}=\widehat{CND}\)(hai góc đối đỉnh)
Do đó: ΔAMN=ΔCND(g-c-g)
b) Xét ΔABC có
M là trung điểm của BA(gt)
N là trung điểm của AC(Gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra:MN//BC

a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp

Ai trả lời hộ điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinhanh lênnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn