+ Phân thức: mẫu số khác ;
+ Căn thức: biểu thức trong căn không âm;
+ Hàm số lượng giác.
2. Sự biến thiên+ Xét chiều biến thiên của hàm số:
Tính đạo hàm ;
Tìm các điểm mà tại đó đạo hàm bằng hoặc không xác định;
Xét dấu đạo hàm suy ra chiều biến thiên của hàm số.
+ Tìm cực trị.
+ Tìm các giới hạn vô cực, các giới hạn tại vô cực và tiệm cận (nếu có).
+ Lập bảng biến thiên.
3. Đồ thị+ Tìm giao điểm của đồ thị với các trục tọa độ;
+ Dựa vào các yếu tố ở trên để vẽ đồ thị;
+ Chú ý thêm tính chẵn, lẻ và tính tuần hoàn (nếu có).
II. Khảo sát hàm số bậc ba dạng , Ví dụ: Khảo sát hàm số1) Tập xác định .
2) Sự biến thiên
+ Chiều biến thiên:
Luyện tập...Kiểm tra
Ta có
Luyện tậpNên hàm số đã cho luôn nghịch biếnđồng biến trên khoảng
và hàm số không có cực trịcó cực tiểucó cực đại.
Kiểm tra+ Giới hạn tại vô cực:
;
Luyện tập
+-
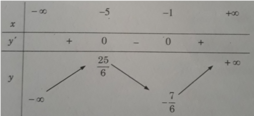
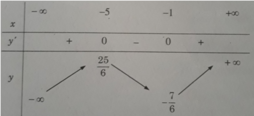
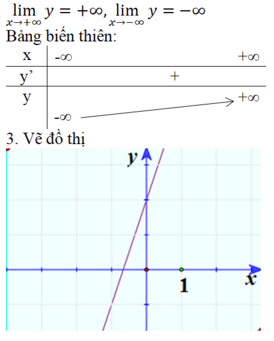
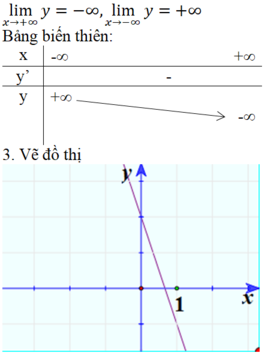
Kiểm tra+ Bảng biến thiên
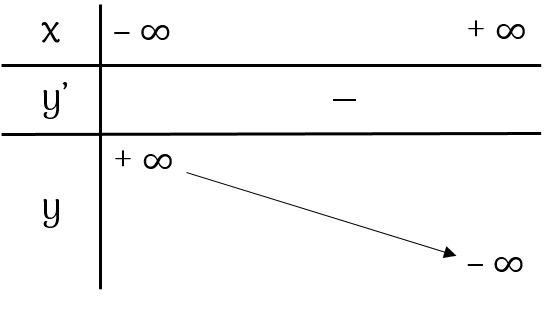
3) Đồ thị
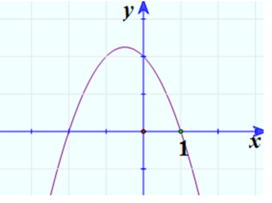
Đồ thị hàm số cắt trục tại điểm .
Luyện tậpvà cắt trục tại điểm (012;-102)
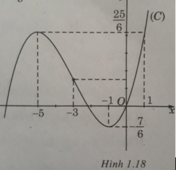
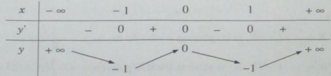
Kiểm traĐồ thị của hàm số đã cho là
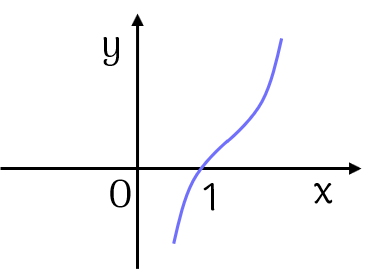
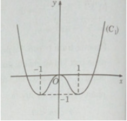
Dạng đồ thị các hàm số dạng ,
.png)
.png)
.png)
+ Phân thức: mẫu số khác ;
+ Căn thức: biểu thức trong căn không âm;
+ Hàm số lượng giác.
2. Sự biến thiên+ Xét chiều biến thiên của hàm số:
Tính đạo hàm ;
Tìm các điểm mà tại đó đạo hàm bằng hoặc không xác định;
Xét dấu đạo hàm suy ra chiều biến thiên của hàm số.
+ Tìm cực trị.
+ Tìm các giới hạn vô cực, các giới hạn tại vô cực và tiệm cận (nếu có).
+ Lập bảng biến thiên.
3. Đồ thị+ Tìm giao điểm của đồ thị với các trục tọa độ;
+ Dựa vào các yếu tố ở trên để vẽ đồ thị;
+ Chú ý thêm tính chẵn, lẻ và tính tuần hoàn (nếu có).
II. Khảo sát hàm số bậc ba dạng , Ví dụ: Khảo sát hàm số1) Tập xác định .
2) Sự biến thiên
+ Chiều biến thiên:
Luyện tập...Kiểm tra
Ta có
Luyện tậpNên hàm số đã cho luôn nghịch biếnđồng biến trên khoảng
và hàm số không có cực trịcó cực tiểucó cực đại.
Kiểm tra+ Giới hạn tại vô cực:
;
Luyện tập
+-
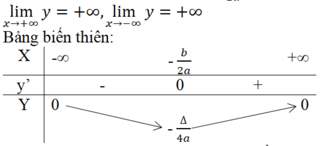
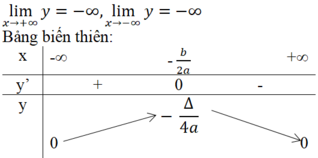
Kiểm tra+ Bảng biến thiên

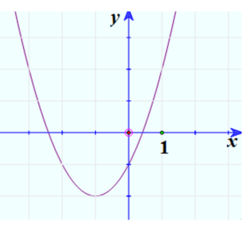
3) Đồ thị
Đồ thị hàm số cắt trục tại điểm .
Luyện tậpvà cắt trục tại điểm (012;-102)
Kiểm traĐồ thị của hàm số đã cho là

Dạng đồ thị các hàm số dạng ,
.png)
.png)
.png)

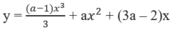
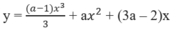
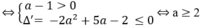
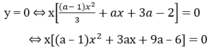
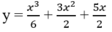
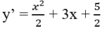
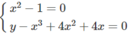
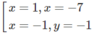
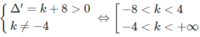
solo tổ hợp xác suất ko ?
2k8 đăng toán 12 cc