Một viên đạn đang bay thẳng đứng lên cao khi đạt vận tốc 10√3 m/s thì nổ thành hai mảnh có khối lượng m1=3m2 mảnh m1 bay theo phương ngang với vận tốc 40m/s hỏi m2 bay theo phương nào với vận tốc bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AM
27 tháng 12 2021
Coi hệ trên là hệ kín, ta có áp dụng bảo toàn động lượng có: \(\overrightarrow{P}=\overrightarrow{P_1}+\overrightarrow{P_2}\)
\(\Rightarrow P_2^2=P_1^2+P^2\Leftrightarrow\left(m_2v_2\right)^2=\left(m_1v_1\right)^2+\left(\left(m_1+m_2\right)v\right)^2\)
\(\Leftrightarrow\left(20v_2\right)^2=\left(10.519\right)^2+\left(30.300\right)^2\)
\(\Rightarrow v_2=519,4615\) (m/s)
Ta có: \(P_1=10.519=5190N\) và \(P_2=20.519,4615=10389,23N\)
Vậy mảnh hai rơi xéo xuống một góc arcsin(5190/10389,23)\(\approx30^0\)so với phương ngang
VT
2 tháng 8 2019
Chọn đáp án C
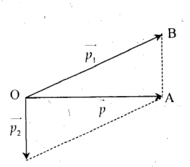
p → = p 1 → + p 2 → → p → ⊥ p 2 → p 1 2 = p 2 2 + p 2 m 1 v 1 2 = m 2 v 2 2 + m v 2 ⇒ v 1 = m 2 v 2 2 + m v 2 m 1 → T h a y s ố v 1 = 4.225 2 + 12.100 2 8 = 187 , 5 m / s
6 tháng 3 2022
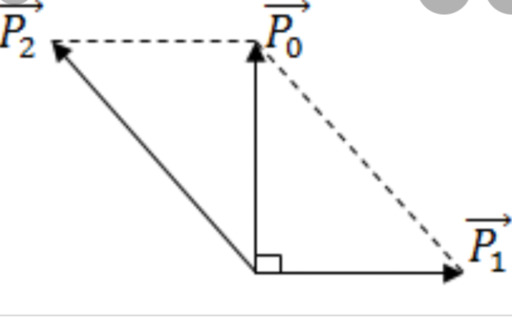
Vận tốc viên đạn trước khi nổ:
\(tan45^o=\dfrac{p}{p_1}=\dfrac{m\cdot v}{m_1\cdot v_1}=\dfrac{2v}{0,5\cdot400}\)
\(\Rightarrow v=100\)m/s
VT
27 tháng 11 2018
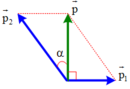
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với p = m v = 2.250 = 500 k g . m / s p 1 = m 1 v 1 = 1.500 = 500 k g . m / s p 2 = m 2 v 2 = v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 500 2 + 500 2 = 500 2 k g m / s
+ Mà sin α = p 1 p 2 = 500 500 2 = 2 2 ⇒ α = 45 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 45 ° với vận tốc 500 2 m / s (m/s)
Chọn đáp án A
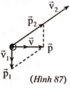
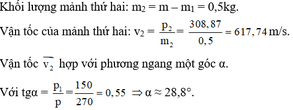
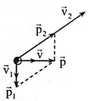
Có \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p_2=\sqrt{p^2+p_1^2}=\sqrt{\left(4m_2.10\sqrt{3}\right)^2+\left(3m_2.40\right)^2}=80\sqrt{3}m_2\)
\(\Rightarrow v_2=80\sqrt{3}\left(m/s\right)\)
Có \(\cos\alpha=\frac{p}{p_2}=\frac{4m_2.10\sqrt{3}}{80\sqrt{3}m_2}=\frac{1}{2}\Rightarrow\alpha=60^0\)
=> p2 hợp với p một góc bằng 600