Lm hộ mik bài kiểm tra với
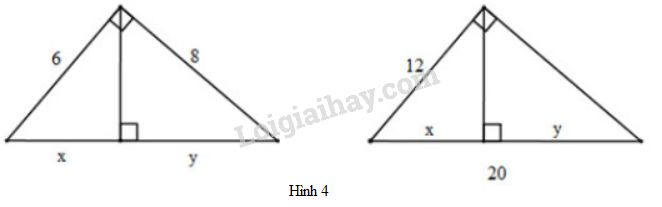
Hãy tính và trong mỗi hình sau (hình :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Hình a
Theo định lí Pitago ta có:
![]()
Áp dụng định lí 1 ta có:
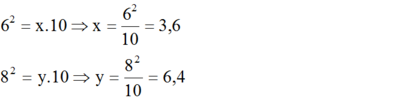
- Hình b
Áp dụng định lí 1 ta có:
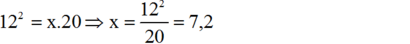
=> y = 20 - 7,2 = 12,8

- Hình a
Theo định lí Pitago ta có:
![]()
Áp dụng định lí 1 ta có:
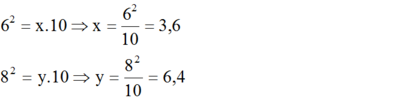
- Hình b
Áp dụng định lí 1 ta có:
![]()
=> y = 20 - 7,2 = 12,8

Đúng hết trừ câu 4 bạn nhé.
\(\sqrt{16x^4y^2}=\sqrt{(4x^2y)^2}=|4x^2y|=4x^2|y|\)

ta co 4a = 5b
\(\Rightarrow\frac{a}{5}=\frac{b}{4}\)
\(\Rightarrow\frac{2a}{10}=\frac{b}{4}\)
áp dung tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{2a}{10}=\frac{b}{4}=\frac{2a-b}{10-4}=\frac{9}{6}=\frac{3}{2}\)
\(\Rightarrow\frac{2a}{10}=\frac{3}{2}\Rightarrow a=7,5\)
\(\frac{b}{4}=\frac{3}{2}\Rightarrow b=6\)
vậy a=7,5 ; b=6
Có b -2a = 9
b = 9 + 2a
Lại có 4a = 5b
4a - 5b = 0
4a - 45 - 10a =0
-6a = 45
a = -7,5
khi đó b = 9 - 2 . 7,5 = -6

Vì số điểm 10 của lớp 4B gấp đôi số điểm 10 của lớp 4A và gấp rưỡi số điểm 10 của lớp 4C và tổng số điểm 10 là 130 nên ta có sơ đồ : ( biểu thị số điểm 10 của lớp 4B là 6 phần bằng nhau), thì số điểm 10 của lớp 4A là 3 phần và số điểm 10 của lớp 4C là 4 phần như thế.
Số điểm 10 lớp 4A là:
130 : (6 + 4 + 3) x 3 = 30 (điểm)
Số điểm 10 lớp 4B là: 30 x 2 = 60 (điểm)
Số điểm 10 lớp 4C là: 130 – 60 – 30 = 40 (điểm)

Tổng số phần bằng nhau là:
7 + 5 = 12 (phần)
Số cây lớp 4A trồng được là:
60 : 12 x 7 = 35 (cây)
Số cây lớp 4B trồng được là:
60 - 35 = 25 (cây)
Em vẽ sơ đồ ra. Lớp 4A 7 phần, 4B 5 phần.
60 cây tương ứng với tổng số phần là 7+5=12 phần
Từ đó tính ra 1 phần ứng với bao nhiêu cây.
Từ đó tính được số cây lớp 4A, 4B

Bài 1: + input: Chiều dài, chiều rộng.
+ output: Diện tích hình chữ nhật.
Bài 2: + input: Số nguyên dương A.
+ output: Là số chẵn hay lẻ.
Bài 3: + input: Ba số nguyên dương a,b,c.
+ output: Là 3 cạnh của tam giác hay ko.

Vẽ các tia Bm và Dn lần lượt song song song với xx' như hình.
Suy ra Bm và Dn cũng song song với yy'
Khi đó: A B m ^ = x A B ^ = 60 o (so le trong)
⇒ m B C ^ = 30 o ⇒ B C y ^ = m B C ^ = 30 o .
Lại có: A D n ^ = D A x ' ^ = 45 o ; n D C ^ = D C y ' ^ = 50 o (so le trong).
Do đó: A D C ^ = 95 o .
TL
+) Sử dụng định lí Pytago trong tam giác vuông: ΔABCΔABC vuông tại AA, khi đó: BC2=AC2+AB2BC2=AC2+AB2.
+) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền:
b2=a.b′, c2=a.c′b2=a.b′, c2=a.c′
Lời giải chi tiết
a) Đặt tên các đỉnh của tam giác như hình dưới:
Áp dụng định lí Pytago vào ΔABCΔABC vuông tại AA, ta có:
BC=√AB2+AC2=√62+82=10BC=AB2+AC2=62+82=10
Áp dụng hệ thức lượng vàoΔABCΔABC vuông tại AA, đường cao AHAH, ta có:
AB2=BC.BH⇒BH=AB2BC=6210=3,6AB2=BC.BH⇒BH=AB2BC=6210=3,6
Lại có HC=BC−BH=10−3,6=6,4HC=BC−BH=10−3,6=6,4
Vậy x=BH=3,6x=BH=3,6; y=HC=6,4y=HC=6,4.
b) Đặt tên các đỉnh của tam giác như hình dưới
Áp dụng hệ thức lượng vào ΔABCΔABC vuông tại AA, đường cao AHAH, ta có:
AB2=BH.BC⇔122=20.x⇒x=12220=7,2AB2=BH.BC⇔122=20.x⇒x=12220=7,2
Lại có: HC=BC−BH=20−7,2=12,8HC=BC−BH=20−7,2=12,8
Vậy x=BH=7,2;x=BH=7,2; y=HC=12,8y=HC=12,8.
Ht ông bn
TL
Theo định lí Pitago ta có:
Áp dụng định lí 1 ta có:
- Hình b
Áp dụng định lí 1 ta có:
=> y = 20 - 7,2 = 12,8
Hoktot~