Bài 2: Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. 1 đường thẳng d tiếp xúc với (O) và (O') lần lượt tại B và C.
a) CM: tam giác ABC vuông
b) Gọi M là trung điểm BC. C/m: AM là tiếp tuyến trung của hai đường tròn
c) C/m: góc OMO' = 90°
d) Các tia BA, CA lần lượt cắt đường tròn (O) và (O') tại D và E. Chứng minh: Diện tích tam giác ADE = Diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

11 tháng 3 2020
https://diendantoanhoc.net/index.php?app=core&module=attach§ion=attach&attach_id=20602
Vào link này xem nhé
Học tốt!!!!!!!

CM
29 tháng 5 2018
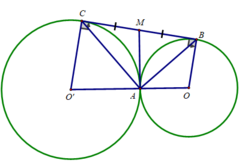
b) Ta có: M là trung điểm của cạnh huyền BC
⇒ MA = MB = MC
⇒ ΔMAB cân tại M ⇒ ∠(MAB ) = ∠(MBA )
Lại có: ΔOAB cân tại O ⇒ ∠(OAB ) = ∠(OBA )
⇒ ∠(MAB ) + ∠(OAB ) = ∠(MBA ) + ∠(OBA ) ⇔ ∠(MAO ) = ∠(MBO) = 90 0
⇒ MA là tiếp tuyến của (O)
Chứng minh tương tự: MA là tiếp tuyến của (O')
Vậy MA là tiếp tuyến chung của hai đường tròn (O) và (O')