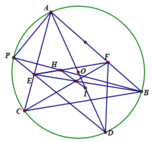
Cho tam giác DEF có 3 góc nhọn nội tiếp đường tròn (O) với DE

NH

Nguyễn Hoàng Minh Vy

20 tháng 2 2020

Cho tam giác DEF có 3 góc nhọn nội tiếp đường tròn (O) với DE<DE và DH là đường cao. Kẻ phân giác góc D cắt đường tròn (O) tại P. Qua F kẻ tiếp tuyến với đường tròn (O) cắt EP kéo dài ở K. a) Chứng minh DP là tia phân giác góc ODH b) PO cắt È tại M và cắt đường tròn (O) tại Q. Kẻ OG⊥QF (G∈QF) . Chứng minh tứ giác OMFG nội tiếp 1 đường tròn tiếp xúc với đường tròn (O) tại F. c) Chứng minh EP=2OG d) Chứng minh...

Đọc tiếp

#Toán lớp 9

0

J

jhhdf

31 tháng 3 2018 - olm

Cho tam giác DEF nhọn nội tiếp đường tròn tâm (O). Vẽ DI vuông góc với EF, IK vuông góc với DE, IH vuông góc với DF

a) c/m DKIH nội tiếp đường tròn và xác định tâm của đường tròn đó

b) C/m \(\widehat{DHK}=\widehat{DEI}\)

ai tiếp mình nhja

#Toán lớp 9

1

CC

chikaino channel

31 tháng 3 2018

Ok

Hình bạn tự vẽ

Câu a

Tứ giác DKIH có

Góc IKD+ Góc IHD = 90°+90°= 180°

=> Tứ gác DKIH nội tiếp

Gọi A là trung điểm DI

∆ IHD vuông có HA là trung tuyến

∆IKD vuông có KA là trung tuyến

=> HA=KA=IA=DA

=> I là tâm đường tròn

Câu b

Tứ giác DKIH nội tiếp

=> góc KHD = Góc DIK

Ta có góc EDI + góc DEI = 90°

Lại có Góc KHI+góc KHD = 90°

Mà góc KDI = Góc KHI (Tứ giác DKIH nội tiếp; cùng chắn cung KI)

=> Cái đề

Đúng(0)

DN

Dũng Nguyễn tiến

7 tháng 6 2021

cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn<O> b BF,CK là các đường cao của tam giác ABC cắt đường tròn <O> tại D,E chứng minh

a, tứ giác BCKF nội tiếp

b, DE // FK

#Toán lớp 9

1

LT

Lê Thị Thục Hiền

7 tháng 6 2021

a) Có \(\widehat{BFC}=\widehat{CKB}=90^0\)

=> Tứ giác BCFK nội tiếp

b)Có \(\widehat{BCK}=\widehat{BFK}\)( vì tứ giác BCFK nội tiếp )

mà \(\widehat{BCE}=\widehat{BDE}=\dfrac{1}{2}sđ\stackrel\frown{EB}\)

=> \(\widehat{BFK}=\widehat{BDE}\) mà hai góc nằm ở vị trí hai góc đồng vị

=> KF//DE

Đúng(3)

NP

Nguyễn Phước Thịnh

19 tháng 3 2022

Cho tam giác nhọn DEF(DE<DF)nội tiếp trong đường tròn(O;R)ba đường cao DK,EM,FN cắt nhau tại H a)Chứng minh DMHN,DMKE là các tứ giác nội tiếp b)Vẽ đường kính DS của đường tròn O.Chứng minh tam giác DFK đồng dạng với tam giác DSE

c)chứng minh OF vuông góc với KM

Giúp mk với sắp kt rùi:((

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

11 tháng 1

a: Xét tứ giác DMHN có \(\widehat{DMH}+\widehat{DNH}=90^0+90^0=180^0\)

nên DMHN là tứ giác nội tiếp

Xét tứ giác DMKE có \(\widehat{DME}=\widehat{DKE}=90^0\)

nên DMKE là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{DFE}\) là góc nội tiếp chắn cung DE

\(\widehat{DSE}\) là góc nội tiếp chắn cung DE

Do đó: \(\widehat{DFE}=\widehat{DSE}\)

Xét (O) có

ΔDES nội tiếp

DS là đường kính

Do đó: ΔDES vuông tại E

Xét ΔDES vuông tại E và ΔDKF vuông tại K có

\(\widehat{DSE}=\widehat{DFK}\)

Do đó: ΔDES đồng dạng với ΔDKF

c: Kẻ tiếp tuyến Fx của (O)

Xét (O) có

\(\widehat{xFE}\) là góc tạo bởi tiếp tuyến Fx và dây cung FE

\(\widehat{EDM}\) là góc nội tiếp chắn cung EF

Do đó: \(\widehat{xFE}=\widehat{EDM}\)

mà \(\widehat{EDM}=\widehat{MKF}\left(=180^0-\widehat{MKE}\right)\)

nên \(\widehat{xFE}=\widehat{MFK}\)

mà hai góc này là hai góc ở vị trí so le trong

nên MK//Fx

Ta có: MK//Fx

OF\(\perp\)Fx

Do đó: OF\(\perp\)MK

Đúng(0)

NN

Nguyễn Ngọc Vi

13 tháng 3 2022

Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O) Hai đường cao BD và CE cắt nhau tại H.Chứng minh rằng:
a.Tứ giác BEDC,AEHD là tứ giác nội tiếp;
b.DEC=DBC
c.Qua A vẽ tiếp tuyến xy của (O) chứng minh OA vuông góc với DE

#Toán lớp 9

0

PT

Pham Trong Bach

8 tháng 3 2019

Cho tam giác ABC nhọn nội tiếp đường tròn (O). H là trực tâm của tam giác ABC.AD là đường kính của (O). E thuộc AC sao cho HE//BC.1). Chứng minh rằng các đường thẳng BH và DE cắt nhau trên (O)2). Gọi F là giao điểm của các đường thẳng EH và AB. Chứng minh rằng A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF3). Gọi I là tâm đường tròn nội tiếp của tam giác DEF. Chứng minh rằng...

Đọc tiếp

#Toán lớp 10

1

CM

Cao Minh Tâm

8 tháng 3 2019

1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.

Ta có A P H ^ = A E H ^ (góc nội tiếp)

= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)

⇒ P H ≡ P B

2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^

Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF

Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF

Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF

3). Do I là tâm nội tiếp nên EI là tia phân giác trong.

Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B

Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.

Đúng(1)

HV

Hak V

26 tháng 3 2015 - olm

đường tròn tâm O ngoại tiếp tam giác nhọn ABC có 2 đường cao BB' và CC' cắt nhau tại H . Gọi D và E lần lượt là giao điểm của BB' và CC' với đừng tròn tâm O
a) Cm BCB'C' nội tiếp đường tròn . XĐ tâm O' của đường tròn này
b) Cm cung AD= cung AE từ đó => OA vuông góc DE
c) AH cắt (O) tại F. Cm H là tâm của đường tròn nội tiếp tam giác DEF

#Toán lớp 9

0

WS

Win S

26 tháng 3 2022

Cho tam giác ABC nhọn nội tiếp đường tròn (o) có 3 đường cao AD;BE;CF cắt nhau tại H. BE cắt đường tròn (o) tại N,gọi M là điểm đối xứng của H qua D
Chứng minh:
a)Tứ giác DHEC;BCEF nội tiếp
b)Tam giác MCN cân
c)EH là phân giác góc DEF

#Toán lớp 9

1