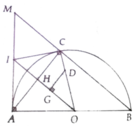
Cho đường tròn tâm O đường kính AB, gọi d là tiếp tuyến ( O) tại A. Trên d lấy M, đường thẳng MB cắt ( O) tại điểm thứ 2 là C. Tiếp tuyến của ( O) tại C cắt d tại I. CMR:
a) Bốn điểm O, I, A, C ,cùng thuộc 1 đường tròn
b) I là trung điểm của AM
c) MB. MC = OM2 - AB2/ 4
d) Trọng tâm G của tam giác AOC luôn cách đều 1 điểm cố định khi M thay đổi trên d