cho tam giác ABC có cạnh A <90 độ . vẽ ra phía ngoai tam giác đó 2 đoạn thẳng AD,AE sao cho :
AD vuông góc vàbằng AB
AEvuông góc và bằng AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A
NH
1
22 tháng 1 2022
\(\widehat{C}=180^0-50^0-65^0=65^0=\widehat{B}\)
=>ΔABC cân tại A
23 tháng 1
ΔABC~ΔA'B'C'
=>\(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
=>\(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\)
=>AB là cạnh nhỏ nhất trong ΔABC
Theo đề, ta có: AB=3cm
=>\(\dfrac{AC}{4}=\dfrac{BC}{5}=\dfrac{3}{3}=1\)
=>\(AC=4\cdot1=4\left(cm\right);BC=5\cdot1=5\left(cm\right)\)
21 tháng 12 2021
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 2 2022
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
22 tháng 9 2023
Tham khảo:
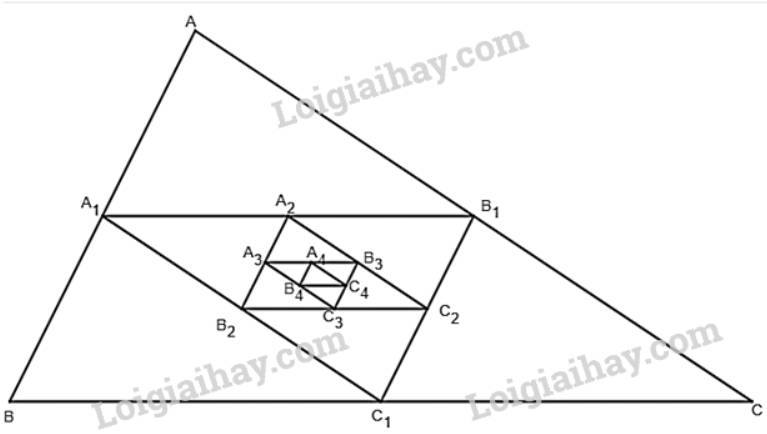
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
26 tháng 10 2018
a) Ta có AB^2+AC^2=6^2+8^2=100=10^2=BC^2
Vậy tam giác ABC vuông b)theo mình thì chứng minh da=de mới đúng
Xét tam giác BAD và tam giác BED có ^BAD=^BED(=90 độ)
Cạnh BD chung ^ABD=^DBE( hai tia phân giác )
Vậy tam giác BAD =tam giác BED =>AD=ED