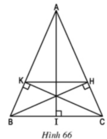
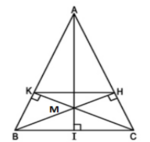
Cho tam giác ABC cân tại A, kẻ đường cao BH và Ck. Tính độ dài cạnh HK, biết BC=12,8cm và AC=24,5cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C H K I
a, tg ABC cân tại A (gt) => ^ABC = ^ACB (tc)
xét tg HCB và tg KBC có : BC chung
^CHB = ^BKC = 90
=> tg ABC = tg KBC (ch-gn)
=> CH = BK (đn)
=> CH/AB = BK/AB mà AB = AC do tam giác ABC cân tại A (Gt)
=> CH/AC = BK/AB
=> HK // BC (đl)
b, sửa đề thành HC.AC = BC.IC
xét tg CHB và tg CIA có : ^ACB chung
^CHB = ^AIC = 90
=> tg CHB đồng dạng với tg AIC (g-g)
=> HC/BC = IC/AC (đn) => HC.AC = BC.IC
c, tg ABC cân tại A (Gt) mà AI là đường cao (gt)
=> AI đồng thời là đtt (đl) => IB = IC = 1/2 BC
mà có : HC.AC = BC.IC (Câu b) ; BC = a; AC = b
=> HC.b = a.a/2 => BC = a^2/2b
Có AH = AC - HC
=> AH = b - a^2/2b = (2b^2 - a^2)/2b
mà HK // BC (câu a) nên
AH/AC = HK/BC => HK = AH.BC/AC = a/b.(2b^2 - a^2)/2b
=> HK = (2ab^2 - a^3)/2b^2 = a - a^3/2b^2

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

a) Xét ΔBKC vuông tại K và ΔCHB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)(ΔABC cân tại A)
Do đó: ΔBKC=ΔCHB(cạnh huyền-góc nhọn)
Suy ra: BK=CH(hai cạnh tương ứng)
b) Xét ΔAIC vuông tại I và ΔBHC vuông tại H có
\(\widehat{BCH}\) chung
Do đó: ΔAIC\(\sim\)ΔBHC(g-g)
Suy ra: \(\dfrac{CA}{CB}=\dfrac{CI}{CH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(CA\cdot CH=CB\cdot CI\)(đpcm)