Giải phương trình x(x+2)(x2+2x+5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
18 tháng 7 2021
\(a,=>x^3-2x^2+4x+2x^2-4x+8-x^3+2x-15=0\)
\(< =>2x-7=0< =>x=\dfrac{7}{2}\)
b,\(=>x\left(x^2-25\right)-\left(x+2\right)\left(x^2-2x+4\right)-3=0\)
\(< =>x^3-25x-x^3+2x^2-4x-2x^2+4x-8-3=0\)
\(< =>-25x-11=0\)
\(< =>x=-0,44\)
PT
1
CM
16 tháng 8 2018
(x2 + 2x – 5)2 = (x2 – x + 5)2
⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ [(x2 + 2x – 5) – (x2 – x + 5)].[(x2 + 2x – 5) + (x2 – x + 5)] = 0
⇔ (3x – 10)(2x2 + x ) = 0
⇔ (3x-10).x.(2x+1)=0
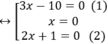
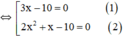
+ Giải (1): 3x – 10 = 0 ⇔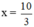 
+ Giải (2):
23 tháng 2 2021
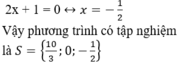
tham khảo
https://hoidapvietjack.com/q/57243/giai-cac-phuong-trinh-sau-a-2x12-2x-12-b-x2-3x-2-5x2-3x60
TM
23 tháng 2 2021
b) (2x+1)2-2x-1=2
\(< =>4x^2+4x+1-2x-1=2\)
\(< =>4x^2+2x-2=0\)
\(< =>4x^2+4x-2x-2=0\)
\(< =>\left(4x^2+4x\right)-\left(2x+2\right)=0\)
\(< =>4x\left(x+1\right)-2\left(x+1\right)=0\)
\(< =>\left(x+1\right)\left(4x-2\right)=0\)
\(=>\left\{{}\begin{matrix}x+1=0=>x=-1\\4x-2=0=>x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy....
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
Đặt \(\sqrt{x^2-2x+5}=t>0\)
\(\Rightarrow x^2-2x=t^2-5\)
Phương trình trở thành:
\(t=t^2-5-1\Leftrightarrow t^2-t-6=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2-2x+5}=3\)
\(\Rightarrow x^2-2x+5=9\)
\(\Rightarrow x^2-2x-4=0\)
\(\Rightarrow...\)
NN
2
Y
11 tháng 4 2022
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
11 tháng 4 2022
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
A4
1
15 tháng 5 2023
a: =>4x^2-24x+36-4x^2+4x-1<10
=>-20x<10-35=-25
=>x>=5/4
b: =>x(x^2-25)-x^3-8<=3
=>x^3-25x-x^3-8<=3
=>-25x<=11
=>x>=-11/25
DA
2
TG
16 tháng 1 2021
a) \(x^2+2x=\left(x-2\right).3x\)
\(\Leftrightarrow x^2+2x=3x^2-6x\)
\(\Leftrightarrow x^2+2x-3x^2+6x=0\)
\(\Leftrightarrow-2x^2+8x=0\)
\(\Leftrightarrow-2x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy S = {0;4}
b) \(x^3+x^2-x-1=0\)
\(\Leftrightarrow x^2\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x^2-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\mp1\end{matrix}\right.\)
Vậy: S = {-1; 1}
c) \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+5\right)\right]\left[\left(x+2\right)\left(x+4\right)\right]=40\)
\(\Leftrightarrow\left(x^2+5x+x+5\right)\left(x^2+4x+2x+8\right)=40\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)=40\)
Đặt x2 + 6x + 5 = t
\(\Leftrightarrow t.\left(t+3\right)=40\)
\(\Leftrightarrow t^2+3t=40\)
\(\Leftrightarrow t^2+2.t.\dfrac{3}{2}+\dfrac{9}{4}=\dfrac{169}{4}\)
\(\Leftrightarrow\left(t+\dfrac{3}{2}\right)^2=\dfrac{169}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}t+\dfrac{3}{2}=\dfrac{13}{2}\\t+\dfrac{3}{2}=-\dfrac{13}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{13}{2}-\dfrac{3}{2}=\dfrac{10}{2}=5\\t=-\dfrac{13}{2}-\dfrac{3}{2}=-\dfrac{16}{2}=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+6x+5=5\\x^2+6x+5=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+6x=0\\x^2+6x+13=0\end{matrix}\right.\)
Mà: \(x^2+6x+13=x^2+2.x.3+9+4=\left(x+3\right)^2+4\ne0\)
=> x2 + 6x = 0
<=> x. (x + 6) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy S = {0; -6}
16 tháng 1 2021
a) Ta có: \(x^2+2x=\left(x-2\right)\cdot3x\)
\(\Leftrightarrow x\left(x+2\right)-3x\left(x-2\right)=0\)
\(\Leftrightarrow x\left[\left(x+2\right)-3\left(x-2\right)\right]=0\)
\(\Leftrightarrow x\left(x+2-3x+6\right)=0\)
\(\Leftrightarrow x\left(-2x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\-2x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\-2x=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy: S={0;4}
b) Ta có: \(x^3+x^2-x-1=0\)
\(\Leftrightarrow x^2\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\cdot\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\cdot\left(x-1\right)\cdot\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Vậy: S={-1;1}
c) Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)
\(\Leftrightarrow\left(x+1\right)\left(x+5\right)\left(x+2\right)\left(x+4\right)-40=0\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)-40=0\)
\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)+40-40=0\)
\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)=0\)
\(\Leftrightarrow\left(x^2+6x\right)\left(x^2+6x+13\right)=0\)
\(\Leftrightarrow x\left(x+6\right)\left(x^2+6x+13\right)=0\)
mà \(x^2+6x+13>0\forall x\)
nên \(x\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy: S={0;-6}
21 tháng 3 2021
\(\dfrac{1}{x+2}\)+\(\dfrac{5}{x-2}\)=\(\dfrac{2x-12}{x^2-4}\)
(đkxđ: x≠2, x≠-2)
⇔ \(\dfrac{x-2}{x^2-4}\)+\(\dfrac{5\left(x+2\right)}{x^2-4}\)= \(\dfrac{2x-12}{x^2-4}\)
⇔ x-2+5(x+2)=2x-12
⇔ x-2+5x+10=2x-12
⇔ 4x=-20
⇔ x=-5(tm)
16 tháng 1 2021
\(a,\left(2x-3\right)^2=\left(x+1\right)^2\\ \Leftrightarrow\left(2x-3\right)^2-\left(x+1\right)^2=0\\ \Leftrightarrow\left(2x-3+x+1\right)\left(2x-3-x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(x-4\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=2\\x=4\end{matrix}\right. \\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=4\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{2}{3};4\right\}\)
16 tháng 1 2021
\(b,x^2-6x+9=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2-9\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-3^2\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left[3\left(x-1\right)\right]^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left(3x-3\right)^2=0\\ \Leftrightarrow\left(x-3+3x-3\right)\left(x-3-3x+3\right)=0\\ \Leftrightarrow-2x\left(4x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-2x=0\\4x-6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\4x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{0;\dfrac{3}{2}\right\}\)
Bạn ơi viết thiếu đề kìa !
xin lỗi nha
đề là x(x+2)(x2+2x+5)=6