 Cho hình vẽ và cho biết: BD = 8cm, AB = 10cm, AC = 17cm. Lấy K thuộc cạnh AE. CMR: AC2-AB2=KC2-KB22
Cho hình vẽ và cho biết: BD = 8cm, AB = 10cm, AC = 17cm. Lấy K thuộc cạnh AE. CMR: AC2-AB2=KC2-KB22
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABH có:
AB^2 = BC.BH
hay 6^2 = 10.BH
suy ra: BH=3,6 (cm)
Tương tự: xét tam giác AHC có:
AC^2 = BC.HC
hay 8^2 = 10.HC
suy ra: HC=6,4 (cm)
Trong tam giác AHC có:
AC^2 = AH^2 + HC^2
hay 10^2 = AH^2 + 6,4^2
suy ra: AH= 7,7 (cm)
MÌNH BIẾT ĐƯƠC CÓ NHIÊU ĐÂY À, CHỪNG NÀO NGHĨ RA THÌ MÌNH LÀM THÊM NHA..!!!

a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).

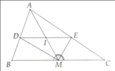

Xét \(\Delta\) ABE vuông tại E, áp dụng định lí Py-ta-go
\(\Rightarrow\)AB2=AE2+EB2
\(\Rightarrow\)AE2=AB2-EB2
Xét ACE vuông tại E, áp dụng định lí Py-ta-go
\(\Rightarrow\)AC2=AE2+CE2
Thay AE2=AB2-EB2 vào công thức
\(\Rightarrow\)AC2=AB2-EB2+CE2
\(\Rightarrow\)AC2-AB2=CE2-EB2 (1)
Xét \(\Delta\) KBE vuông tại E, áp dụng định lí Py-ta-go
\(\Rightarrow\)KB2=KE2+EB2
\(\Rightarrow\)KE2=KB2-EB2
Xét KCE vuông tại E, áp dụng định lí Py-ta-go
\(\Rightarrow\)KC2=KE2+CE2
Thay KE2=KB2-EB2 vào công thức
\(\Rightarrow\)KC2=KB2-EB2+CE2
\(\Rightarrow\)KC2-KB2=CE2-EB2 (2)
Từ (1) và (2) \(\Rightarrow\) AC2-AB2=KC2-KB2 (=CE2-EB2)
CHÚC BẠN HỌC TỐT !