CMR: Với mọi a thì đồ thị của hàm số \(y=ax^2+\left(4a-2\right)x+3a\) luôn đi qua hai điểm cố định.
Tìm tọa độ của hai điểm đó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
]
20 tháng 11 2016
a/ Hai hàm số có đồ thị // với nhau khi
\(\hept{\begin{cases}m-2=1\\3\ne0\end{cases}}\Leftrightarrow m=3\)
b/ Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ
\(\hept{\begin{cases}y=x+3\\y=2x+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)
c/ Gọi điểm mà đường thẳng luôn đi qua là M(a,b) ta thế vào hàm số được
\(b=ma+3\)
\(\Leftrightarrow ma+3-b=0\)
Để phương trình này không phụ thuôc m thì
\(\hept{\begin{cases}a=0\\3-b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=0\\b=3\end{cases}}\)
Tọa độ điểm cần tìm là M(0, 3)
20 tháng 11 2016
d/ Ta có khoản cách từ O(0,0) tới (d) là 1
\(\Rightarrow=\frac{\left|0-0m-3\right|}{\sqrt{1^2+m^2}}=\frac{3}{\sqrt{1+m^2}}=1\)
\(\Leftrightarrow\sqrt{1+m^2}=3\)
\(\Leftrightarrow m^2=8\)
\(\Leftrightarrow\orbr{\begin{cases}m=2\sqrt{2}\\m=-2\sqrt{2}\end{cases}}\)
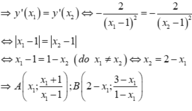
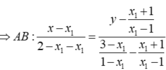
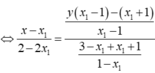
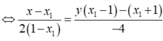
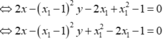
\(y=ax^2+\left(4a-2\right)x+3a\)
\(\Leftrightarrow ax^2+4ax-2x+3a-y=0\)
\(\Leftrightarrow a\left(x^2+4x+3\right)-2x-y=0\)
Vì pt trên luôn đúng với mọi \(a\) nên ta có:
\(\left\{{}\begin{matrix}x^2+4x+3=0\\2x+y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+1\right)\left(x+3\right)=0\\y=-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=-3\\y=6\end{matrix}\right.\end{matrix}\right.\)
Giả sử đường thẳng trên đi qua 2 điểm cố định. Gọi tọa độ của 2 điểm đó lần lượt là \(A\left(x_1;y_1\right)\) và \(B\left(x_2;y_2\right)\)
Khi đó: \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x_1=-1\\y_1=2\end{matrix}\right.\\\left\{{}\begin{matrix}x_2=-3\\y_2=6\end{matrix}\right.\end{matrix}\right.\)
Vậy 2 điểm cố định thuộc đường thẳng đó có tọa độ là \(\left(-1;2\right)\) và \(\left(-3;6\right)\).