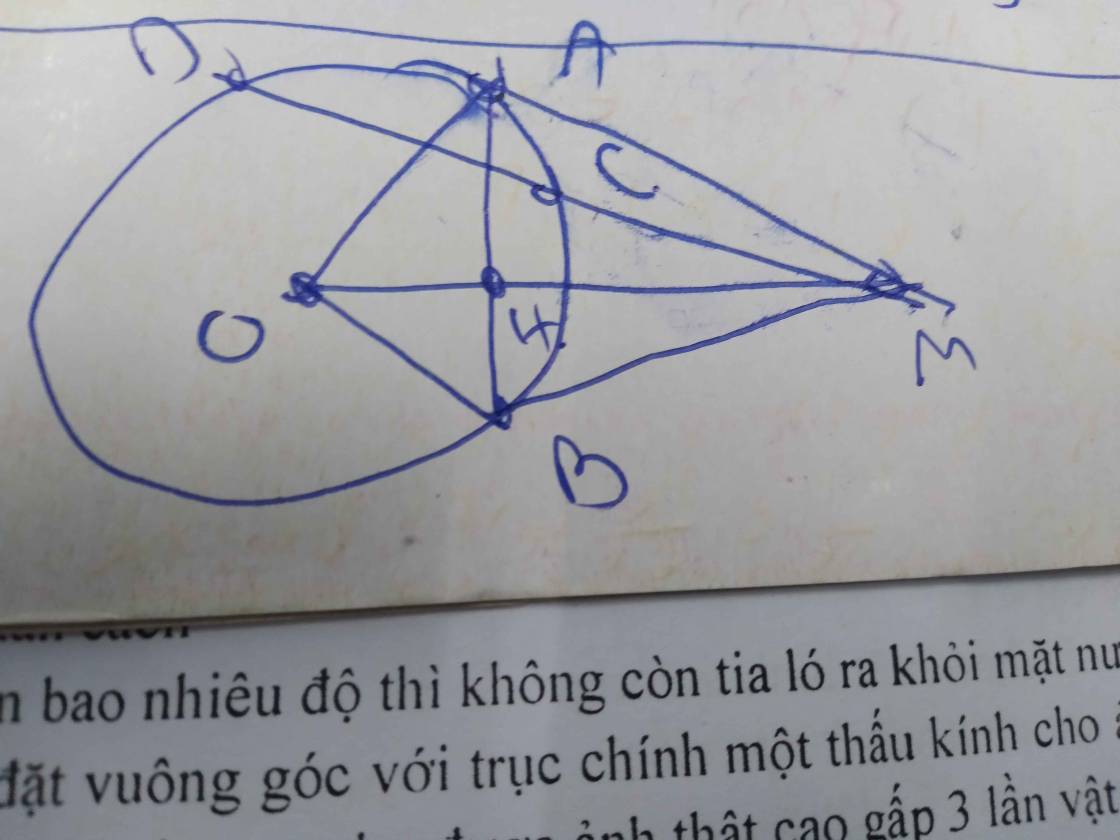
Cho đường tròn (O,R) và điểm M nằm ngoài đường tròn. Vẽ các tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm) và cát tuyến MCD không đi qua tâm O(C nằm giữa). Gọi I là trung điểm của CD
a, Chứng minh AMBI nội tiếp
b, Đường thẳng qua C vuông góc với OA cắt AB,AD lần lượt ở N,K. Chứng minh BCNI nội tiếpvà Nlà trung điểm của CK
c, Gọi Q là giao điểm của AB và MD. Chứng minh \(\frac{QC}{QD}=\frac{MC}{MD}\)