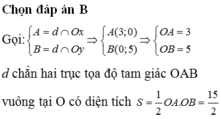Đường thẳng 6x+5y=30 tạo với các trục tọa độ một Tam giác có diện tích bằng bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
9 tháng 6 2021
Gọi giao của đường thẳng và trục Ox là A => A(m+1;0)
=> OA = | m+1 |
Gọi giao của đường thẳng với trục Oy là B => B(0 ; m+1)
=> OB=|m+1|
Theo đề bài ta có S ABC =8
<=> 1/2 x OA x OB= 8
<=> 1/2 x |m+1| x |m+1| = 8
từ đó giải ra m=3
#HT#
CM
3 tháng 12 2018
+ Giao điểm của đồ thị hàm số y= 2x-3 với trục hoành là điểm A( 3/2; 0).
+ Giao điểm của đồ thị hàm số y= 2x-3 với trục tung là điểm B( 0; -3).
+ Đường thẳng ∆ tạo với hai trục tọa độ ∆ OAB vuông tại O. Suy ra
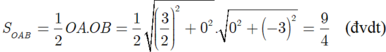
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2021
Gọi A và B lần lượt là giao điểm của d với Ox và Oy
\(\Rightarrow A\left(-\dfrac{1}{m^2+2};0\right)\) ; \(B\left(0;1\right)\) \(\Rightarrow OA=\dfrac{1}{m^2+2}\) ; \(OB=1\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{8}\Leftrightarrow OA.OB=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{m^2+2}=\dfrac{1}{4}\Rightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)