Giải phương trình:
x3 - x2y + 2x - y = 2 (x,y là các số nguyên)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 6 2017
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12
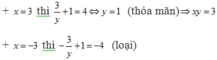
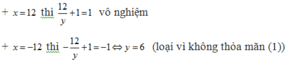
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
TD
19 tháng 7 2021
bài 2 :
x3+7y=y3+7x
x3-y3-7x+7x=0
(x-y)(x2+xy+y2)-7(x-y)=0
(x-y)(x2+xy+y2-7)=0
\(\left\{{}\begin{matrix}x-y=0\Rightarrow x=y\left(loại\right)\\x^{2^{ }}+xy+y^2-7=0\end{matrix}\right.\)
x2+xy+y2=7 (*)
Giải pt (*) ta đc hai nghiệm phan biệt:\(\left[{}\begin{matrix}x=1va,y=2\\x=2va,y=1\end{matrix}\right.\)
KN
2
HP
31 tháng 8 2021
\(x^3-x+24=0\)
\(\Leftrightarrow x^3+3x^2-3x^2-9x+8x+24=0\)
\(\Leftrightarrow x^2\left(x+3\right)-3x\left(x+3\right)+8\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+8\right)=0\)
\(\Leftrightarrow x=-3\)
31 tháng 8 2021
Ta có: \(x^3-x+24=0\)
\(\Leftrightarrow x^3+3x^2-3x^2-9x+8x+24=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+8\right)=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3
T
0
24 tháng 12 2019
Đáp án A
Đặt số proton của X, Y là ZX, ZY
Ta có 2ZX + ZY = 23 (1)
- Nếu X trước Y thì ZY = ZX + 1 (2)
Từ (1) và (2) → 2ZX + ZX + 1 = 23→ ZX = 22/3 = 7,3 (vô lí)
- Nếu Y trước X thì ZX = ZY + 1 (3)
Từ (1) và (3) → 2( ZY + 1) + ZY = 23 → 3ZY = 21
ZY = 7 → Y là nito (N)
ZX = 8 → X là oxi (O)
Công thức X2Y là NO2
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
\(\left(x^2y-8x+y-4\right)log_3y=2log_3\dfrac{\sqrt{8x-y+4}}{x}-log_3y=log_3\dfrac{8x-y+4}{x^2y}\)
\(\Rightarrow log_3\left(x^2y\right)+x^2y.log_3y=log_3\left(8x-y+4\right)+\left(8x-y+4\right)log_3y\)
Xét hàm \(f\left(t\right)=log_3t+t.log_3y\Rightarrow f'\left(t\right)=\dfrac{1}{1.ln3}+log_3y>0\)
\(\Rightarrow x^2y=8x-y+4\)
\(\Rightarrow y=\dfrac{8x+4}{x^2+1}\)
Tìm y để pt trên có nghiệm lớn hơn 1, lập BBT \(\Rightarrow y< 6\)
NQ
1
30 tháng 1 2021
Ta có: \(\left(2x+3y\right)^2< \left(2x+3y\right)^2+5x+5y+1< \left(2x+3y+2\right)^2\).
Do đó để \(\left(2x+3y\right)^2+5x+5y+1\) là số chính phương thì \(\left(2x+3y\right)^2+5x+5y+1=\left(2x+3y+1\right)^2\Leftrightarrow x=y\).
Vậy x = y