Tổng các số hạn của dãy số vô hạn sau \(1;\frac{-1}{2};\frac{1}{4};-\frac{1}{8};...;\frac{\left(-1\right)^{n+1}}{2^{n-1}};...\) bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Program HOC24;
var m,n,i: byte;
t,d,code: integer;
s,st: string;
begin
write('Nhap N: '); readln(n);
m:=0;
for i:=1 to n do
begin
str(i,s);
st:=st+s;
end;
t:=0;
for i:=1 to n do
begin
val(st[i],d,code);
t:=t+d;
end;
write(t);
readln
end.
program tong;
uses crt;
var n, i, a : integer; x, s : string;
begin
clrscr;
write('nhap n= '); readln(n);
for i:=1 to n do
begin
str(i,s);
x:=x+s;
if length(x)=n then break
end;
{tim n so trong day}
for i:=1 to length(x) do
begin
val(x[i],n);
a:=a+n;
end;
{tinh tong n so trong day}
writeln('tong la ',a);
end.

a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
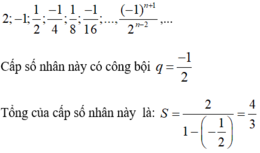


Ta sẽ CM tổng của 2 số chính phương chia 4 không thể có số dư là 3.
Thật vậy mọi số chính phương chẵn luôn chia hết cho 4.
mọi số chính phương lẻ luôn chia 4 dư 1 (vì (2x+1)2=4x(x+1)+1 chia 4 dư 1)
Do đó tổng của hai số chính phương chỉ có thể có số dư 0,1 hoặc 2 khi chia cho 4
Mà các số trên đều được viết dưới dạng 11...1=10...0+11.
Mà 10...0 chia hết cho 4 và 11 chia 4 dư 3 nên dãy số này không có số nào biểu diễn được dưới dạng tổng của 2 số chính phương (đpcm)

Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức 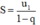

Chọn đáp án C vì dãy ở đây là một CSN có công bội q = 3 2 > 1 ,
nên dãy 3 2 , 9 4 , 27 8 , . . . , 3 2 n , . . . không phải là dãy lùi vô hạn.
Chọn C

Đáp án C
Chọn đáp án C vì dãy ở đây là một CSN có công bội q = 3 2 > 1 , nên dãy 3 2 , 9 4 , 27 8 , . . . , 3 2 n không phải là dãy lùi vô hạn
Dãy đã cho là cấp số nhân vô hạn với \(u_1=1\) và công bội \(q=-\frac{1}{2}\)
Do \(\left|q\right|< 1\) áp dụng công thức tổng cấp số nhân lùi vô hạn:
\(S=\frac{u_1}{1-q}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\)