Một người đi xe đạp trên quãng đường AB. 2/7 đoạn đường đầy đi với vận tốc 20km/h,1/7 đoạn đường tiếp xe đi với vận tốc 36km/h,1/7 đoạn đường tiếp theo đi với vận tốc 24km/h,3/7 đoạn đường cuối đi với vận tốc 15km/h. Tính vận tốc trung bình của xe trên cả đoạn đường AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2021
\(=>t1=\dfrac{\dfrac{1}{3}S}{12}=\dfrac{S}{36}\left(h\right)\)
\(=>t2=\dfrac{\dfrac{1}{3}S}{8}=\dfrac{S}{24}\left(h\right)\)
\(=>t3=\dfrac{\dfrac{1}{3}S}{6}=\dfrac{S}{18}\left(h\right)\)
\(=>vtb=\dfrac{S}{t1+t2+t3}=\dfrac{S}{\dfrac{S}{36}+\dfrac{S}{24}+\dfrac{S}{18}}=\dfrac{S}{\dfrac{432S+648S+864S}{15552}}\)
\(=\dfrac{S}{\dfrac{1944S}{15552}}=\dfrac{15552}{1944}=8km/h\)
HQ
24 tháng 2 2021
Ta có: \(v_{tb}=\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{S}{\dfrac{S}{36}+\dfrac{S}{42}+\dfrac{S}{30}}=\dfrac{1260}{107}\left(km/h\right)\)
24 tháng 2 2021
\(v_{tb}=\dfrac{\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}{\dfrac{\dfrac{1}{3}}{12}+\dfrac{\dfrac{1}{3}}{14}+\dfrac{\dfrac{1}{3}}{10}}=\dfrac{1260}{107}\approx11,776\left(\dfrac{km}{h}\right)\)
5 tháng 7 2016
Vận tốc trung bình của người đi xe đạp trên đoạn đường AB là :
(14+16+8) : 3 = 12,6666..... (km/giờ) \(\approx\)12,67 (km/giờ)
Vậy vận tốc trung bình của người đi xe đạp trên đoạn đường AB là 12,67 km/giờ
TP
25 tháng 12 2022
Tóm tắt:
\(s_1=s_2=s_3=\dfrac{1}{3}s_{AB}\)
\(v_1=13km/h\\ v_2=15km/h\\ v_3=17km/h\)
\(-----\\ v_{TB}=?\)
-- giải ---
Gọi độ dài mỗi đoạn đường là s
Ta có
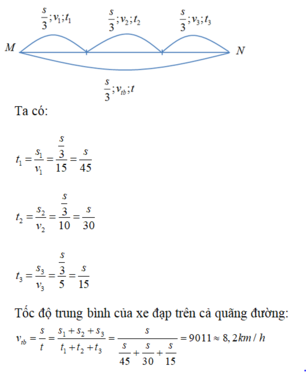
\(v_{TB}=\dfrac{s+s+s}{t_1+t_2+t_3}=\dfrac{s+s+s}{\dfrac{s}{v_1}+\dfrac{s}{v_2}+\dfrac{s}{v_3}}\\ =\dfrac{3s}{s\left(\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}\right)}=\dfrac{3}{\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}}\)
Mình gợi ý cách làm. Đến đây thì bạn có thể thế số và bấm máy tính là tìm đc vTB rồi nhé!
D
5 tháng 10 2018
Thời gian đi 1/3 quãng đường đầu:
t1= \(\dfrac{S}{3v_1}\)
Thời gian đi 1/3 quãng đường giữa:
t2= \(\dfrac{S}{3v_2}\)
Thời gian đi 1/3 quãng đường cuối:
t3= \(\dfrac{S}{3v_3}\)
Vận tốc trung bình trên cả đoạn đường AB là:
vtb= \(\dfrac{S}{t_1+t_2+t_3}\)= \(\dfrac{S}{\dfrac{S}{3v_1}+\dfrac{S}{3v_2}+\dfrac{S}{3v_3}}\)= \(\dfrac{1}{\dfrac{1}{3v_1}+\dfrac{1}{3v_2}+\dfrac{1}{3v_3}}\)
Thay v1, v2 và v3 vào ta được:
vtb= 13,85(km/h)
24 tháng 8 2021
Thời gian đi trên 1/3 đoạn đường đầu là:
\(t_1=\dfrac{AB}{3v_1}=\dfrac{AB}{3.14}=\dfrac{AB}{42}\left(h\right)\)
Thời gian đi trên 1/3 đoạn đường tiếp theo là:
\(t_2=\dfrac{AB}{3v_2}=\dfrac{AB}{3.16}=\dfrac{AB}{48}\left(h\right)\)
Thời gian đi trên 1/3 đoạn đường cuối cùng là:
\(t_3=\dfrac{AB}{3v_3}=\dfrac{AB}{3.8}=\dfrac{AB}{24}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường là:
\(v_{tb}=\dfrac{AB}{t_1+t_2+t_3}=\dfrac{AB}{\dfrac{AB}{42}+\dfrac{AB}{48}+\dfrac{AB}{24}}=\dfrac{AB}{AB\left(\dfrac{1}{42}+\dfrac{1}{48}+\dfrac{1}{24}\right)}=\dfrac{1}{\dfrac{1}{42}+\dfrac{1}{48}+\dfrac{1}{24}}=\dfrac{336}{29}\left(km/h\right)\)
24 tháng 8 2021
\(=>Vtb=\dfrac{S}{t1+t2+t3}=\dfrac{S}{\dfrac{\dfrac{1}{3}S}{v1}+\dfrac{\dfrac{1}{3}S}{v2}+\dfrac{\dfrac{1}{3}S}{v3}}\)
\(=>vtb=\dfrac{S}{\dfrac{S}{42}+\dfrac{S}{48}+\dfrac{S}{24}}=\dfrac{S}{\dfrac{S\left(48.24+42.24+48.42\right)}{48384}}=\dfrac{48384}{4176}=11,6km/h\)
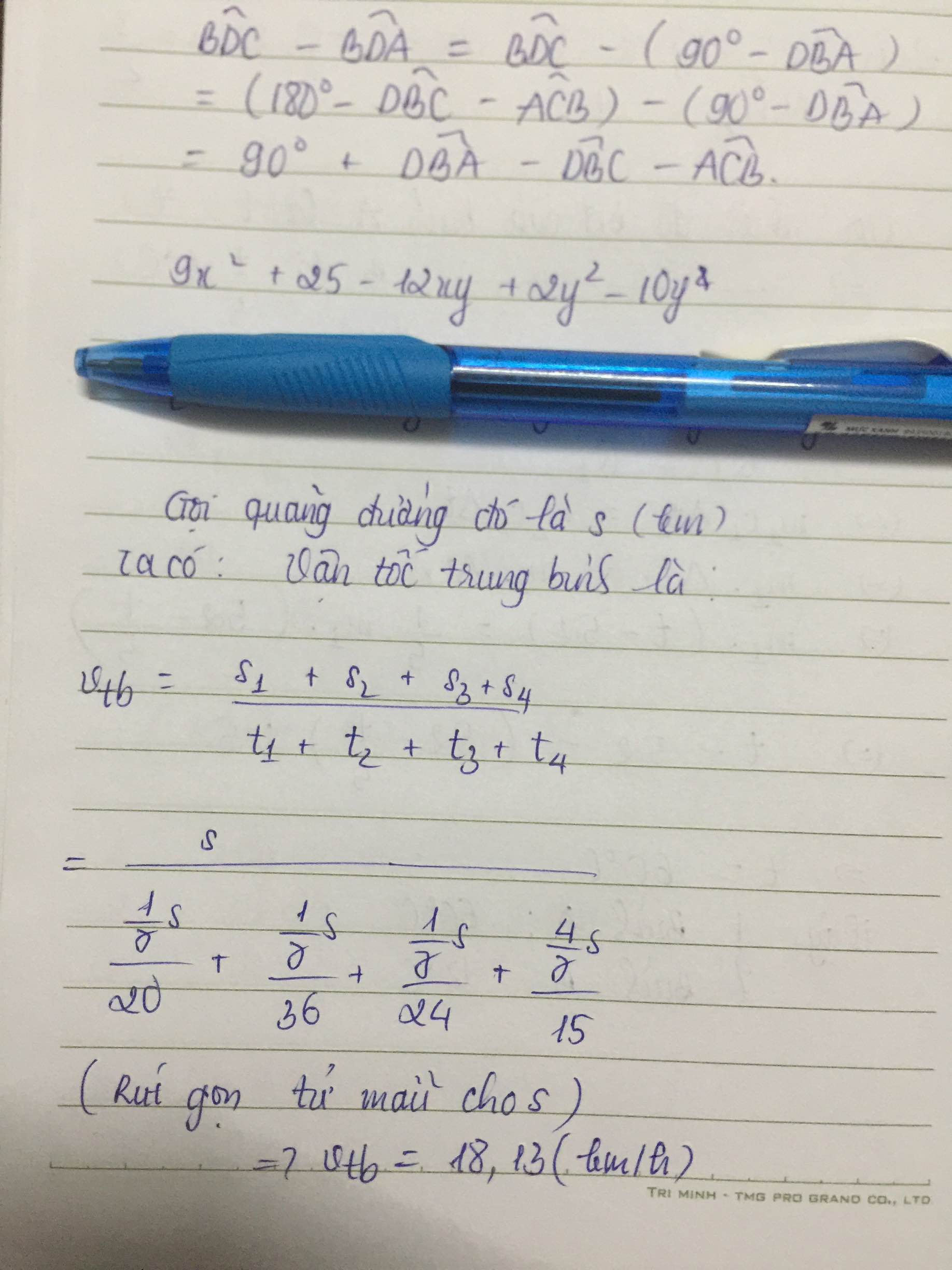
Bài làm :
\(\frac{2}{7}\) đoạn đường đầu xe đạp đi với thời gian là :
\(t_1=\frac{\frac{2s}{7}}{20}=\frac{s}{70}\left(h\right)\)
\(\frac{1}{7}\) đoạn đường tiếp xe đi với thời gian :
\(t_2=\frac{\frac{1s}{7}}{36}=\frac{s}{252}\left(h\right)\)
\(\frac{1}{7}\) đoạn đường tiếp theo xe đi với thời gian :
\(t_3=\frac{\frac{1S}{7}}{24}=\frac{s}{168}\left(h\right)\)
\(\frac{3}{7}\) đoạn đường cuối xe đi với thời gian là :
\(t_4=\frac{\frac{3s}{7}}{15}=\frac{s}{35}\left(h\right)\)
Vận tốc trung bình của xe trên cả đoạn đường AB là :
\(v_{tb}=\frac{\frac{2s}{7}+\frac{1s}{7}+\frac{1s}{7}+\frac{3s}{7}}{\frac{s}{70}+\frac{s}{252}+\frac{s}{168}+\frac{s}{35}}=\frac{360}{19}\approx19km/h\)