Tìm x thuộc Z biết: x2+100x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
22 tháng 7 2017
( x − 2 ) ( x 2 + 2 ) = 0 ⇔ x − 2 = 0 x 2 + 2 = 0 ⇔ x = 2 x 2 = − 2 ( L )
Vậy x = 2
PT
1
CM
8 tháng 3 2018
a) x ( x + 6 ) = 0 ⇔ x = 0 x + 6 = 0 ⇔ x = 0 x = − 6
Vậy x = 0 hoặc x = - 6
b) ( x − 3 ) . ( y + 7 ) = 0 ⇔ x − 3 = 0 y + 7 = 0 ⇔ x = 3 y = − 7
Vậy x = 3 hoặc x = -7
c) ( x − 2 ) ( x 2 + 2 ) = 0 ⇔ x − 2 = 0 x 2 + 2 = 0 ⇔ x = 2 x 2 = − 2 ( L )
Vậy x = 2
7 tháng 2 2020
a) Ta thấy: |x + 1|, |x + 2|, |x + 3|, ..., |x + 98|, |x + 99| lớn hớn hoặc bằng 0 với mọi x
Mà |x + 1| + |x + 2| + |x + 3| +...+ |x + 98| + |x + 99| = 100x
=> 100x lớn hơn hoặc bằng 0 => x lớn hơn hoặc bằng 0
=> |x + 1| + |x + 2| + |x + 3| +...+ |x + 98| + |x + 99| = x + 1 + x + 2 + x + 3 + ... + x + 98 + x + 99
=>x + x + x + ... + x ) + ( 1 + 2 + 3 + ... + 98 + 99 ) = 100x
=> 99x + 2500 = 100x => 2500 = 100x - 99x => x = 2500
b. Ta thấy: \(x-1\ge0\Leftrightarrow x\ge1\) , \(x-5\ge0\Leftrightarrow x\ge5\)
TH1: \(x\ge5\Rightarrow|x-5|=x-5,|x-1|=x-1\)
=> |x - 1| + |x - 5| = x - 1 + x - 5 = 4 => 2x - 6 = 4 => 2x = 10 => x = 5
- Tương tự làm 2 trường hợp nữa là \(x< 1\) và \(1\le x< 5\) là ra nhé :D
YN
7 tháng 2 2020
b) | x - 1 | + | x - 5 | = 4 (1)
Ta có bảng xét dấu
+) Nếu x < 1 thì | x - 1 | + | x - 5 | = ( 1 - x ) + ( 5 - x ) = 1 - x + 5 - x = 6 - 2x
\(\Rightarrow\left(1\right)\Leftrightarrow6-2x=4\)
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\) ( ko thỏa mãn x < 1 )
+) Nếu \(1\le x\le5\) thì | x - 1 | + | x - 5 | = ( x - 1 ) + ( 5 - x ) = x - 1 + 5 - x =4
\(\Rightarrow\left(1\right)\Leftrightarrow4=4\) ( thỏa mãn với mọi \(1\le x\le5\) )
\(\Rightarrow\)\(1\le x\le5\) thỏa mãn đề bài
+) Nếu x > 5 thì | x - 1 | + | x - 5 | = x - 1 + x - 5 = 2x - 6
\(\Rightarrow\left(1\right)\Leftrightarrow2x-6=4\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\) ( ko thỏa mãn x > 5 )
Vậy \(1\le x\le5\) thỏa mãn đề bài
!! Học tốt @@
# Chiyuki Fujito
PT
2
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Bài 4:
a. Ta thấy: $x^2-x+2=(x-\frac{1}{2})^2+1,75>0$ với mọi $x$.
Do đó để $B=\frac{x^2-x+2}{x-3}<0$ thì $x-3<0$
$\Leftrightarrow x<3$
b.
$B=\frac{x(x-3)+2(x-3)+8}{x-3}=x+2+\frac{8}{x-3}$
Với $x$ nguyên, để $B$ nguyên thì $x-3$ phải là ước của 8.
$\Rightarrow x-3\in\left\{\pm 1; \pm 2; \pm 4; \pm 8\right\}$
$\Rightarrow x\in \left\{4; 2; 5; 1; -1; 7; 11; -5\right\}$
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Bài 5:
\(\frac{\frac{x}{x-y}-\frac{y}{x+y}}{\frac{y}{x-y}+\frac{x}{x+y}}=\frac{\frac{x(x+y)-y(x-y)}{(x-y)(x+y)}}{\frac{y(x+y)+x(x-y)}{(x-y)(x+y)}}\)
\(=\frac{x(x+y)-y(x-y)}{y(x+y)+x(x-y)}=\frac{x^2+y^2}{x^2+y^2}=1\)
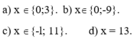
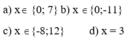
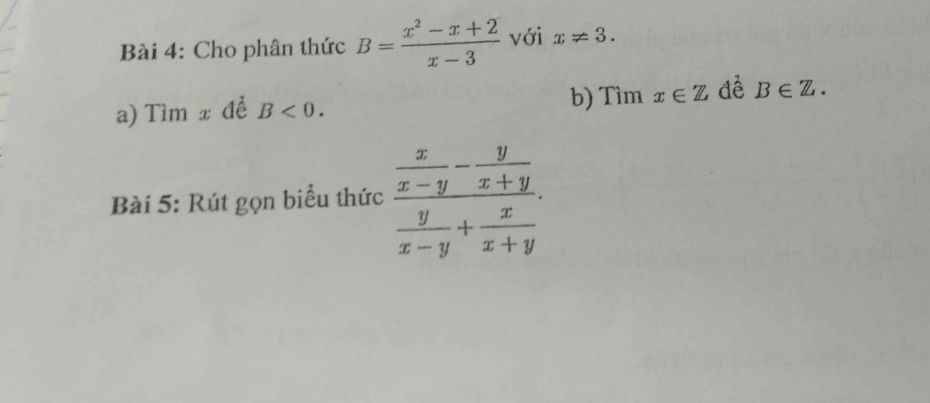
x2+100x=0
x.x+100.x=0
x.(x+100)=0
* x=0 * x+100=0
x=0-100
x=-100
vậ x=0 hoặc x=-100
x^2+100x=0
x.x+100.x=0
x.(x+100)=0
Để x.(x+100)=0=>x hoặc x+100 phải = 0
=>x=0;x=-100
Vậy x=0;x=-100