Một người đưa thư đi từ A đến B và lại quay về A mất 1,4h. Lúc đi từ A đến B vận tốc là 12km/h. Khi về là 6m/s. Tìm độ dài quãng đường từ A đến B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
OC
23 tháng 4 2021
Gọi x(km) là QĐ A-B (x>0)
=> \(\frac{x}{36}\) (h)là thời gian lúc đi đến B
=>\(\frac{x}{45}\)(h) là thời gian khi quay trở lại A
đổi 30p=0.5h
Do thời gian cả đi là về là 5h nên ta có phương trình:
\(\frac{x}{36}\)+\(\frac{x}{45}\)+0.5=5
<=> \(\frac{45x}{1620}\)+\(\frac{36x}{1620}\)+\(\frac{810}{1620}\)=\(\frac{8100}{1620}\)
<=> 45x +36x +810 = 8100
<=> 81x = 7290
<=> x=90 (TM)
Vậy QĐ A-B dài 90Km
22 tháng 4 2021
Gọi độ dài quãng đường AB là x ( km ; x > 0 )
Tổng thời gian đi và về ( không tính thời gian nghỉ ) là : 5h - 30' = 4h30' = 9/2h
Vận tốc lúc về = 36 + 9 = 45km/h
Thời gian lúc đi = x/36 (h)
Thời gian lúc về = x/45 (h)
Tổng thời gian đi và về là 9/2h nên ta có phương trình :
x/36 + x/45 = 9/2
<=> x( 1/36 + 1/45 ) = 9/2
<=> x = 90 (tm)
Vậy độ dài quãng đường AB là 90km
MD
17 tháng 8 2021
Gọi độ dài quãng đường AB là x (km)(x > 0)
Thời gian người đó đi từ A đến B là x/15 (giờ)
Thời gian người đó đi từ B về A là x/12 (giờ)
Vì tổng thời gian đi và về mất 4 giờ 30 phút =\(\dfrac{9}{2}\) giờ nên ta có phương trình:
\(\dfrac{x}{15}+\dfrac{x}{12}=\dfrac{9}{2}\)
\(\Rightarrow4x+5x=270\)
\(\Leftrightarrow9x=270\)
\(\Leftrightarrow x=30\) (thỏa mãn)
Vậy quãng đường AB dài 30 km.
17 tháng 8 2021
Gọi độ dài quãng đường là x
Theo đề, ta có phương trình:
\(\dfrac{x}{15}+\dfrac{x}{12}=\dfrac{9}{2}\)
\(\Leftrightarrow x=30\)
25 tháng 4 2017
Đổi: 4 giờ 30 phút = 4,5 giờ
Tỉ số vận tốc 15km/giờ và vận tốc 12km/giờ là:
15 : 12 = \(\frac{5}{4}\)
Trên cùng 1 quãng đường, vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch
\(\Rightarrow\)Tỉ số thời gian đi bằng \(\frac{4}{5}\)thời gian về.
Coi thời gian đi là 4 phần bằng nhau thì thời gian về là 5 phần như thế.
Vậy thời gian đi là:
4,5 : (4 + 5) x 4 = 2 (giờ)
Chiều dài quãng đường là:
15 x 2 = 30 (km)
Đ/S: 30km
25 tháng 4 2017
Tỉ lệ vận tốc lúc về và lúc đi : 12 : 15 = 4/5
Thời gian người ấy đi : 4 giờ 30 phút = 4,5 giờ
4,5 : ( 4 + 5 ) x 4 = 2 giờ
Quãng đường AB dài : 2 x 15 = 30 km
ĐS : 30 km ( tại sao lại nhân 4 vì thời gian tỉ lệ nghịch với thời gian )
DT
Đỗ Thanh Hải
CTVVIP
2 tháng 3 2021
Gọi vận tốc từ A đến B là x (km/h)(x>0)
Theo bài ta có: \(\dfrac{90}{x}+\dfrac{90}{x+9}+\dfrac{1}{2}=5\)
=> \(\dfrac{90\left(x+9\right)}{x\left(x+9\right)}+\dfrac{90x}{x\left(x+9\right)}=\dfrac{9}{2}\)
=> \(\dfrac{90x+810+90x}{x^2+9x}=\dfrac{9}{2}\)
=> \(\dfrac{180x+810}{x^2+9x}=\dfrac{9}{2}\)
=> \(360x+1620=9x^2+91x\)
=> \(9x^2-269x-1620=0\)
=> x = 36
hoặc x = -5 (loại)
Vậy vtoc xe máy là 36km/h
CM
28 tháng 5 2019
Đổi 4h30’ = 4,5h
Gọi độ dài quãng đường AB là x km (x > 0)
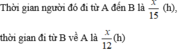
Tổng thời gian đi của xe đạp là 4,5 giờ nên ta có phương trình:
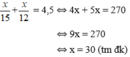
Vậy độ dài quãng đường AB là 30km.
QA
23 tháng 6 2021
Trả lời:
Đổi: \(30ph=\frac{1}{2}h\)
Gọi vận tốc xe máy lúc đi từ A đến B là: x ( km/h; x > 0 )
=> vận tốc xe máy lúc đi từ B về A là: x + 9 ( km/h )
thời gian xe máy đi từ A đến B là: \(\frac{90}{x}\)( giờ )
thời gian xe máy đi từ B về A là: \(\frac{90}{x+9}\)( giờ )
Theo bài ra, ta có:
\(\frac{90}{x}+\frac{90}{x+9}+\frac{1}{2}=5\)
\(\Leftrightarrow\frac{90}{x}+\frac{90}{x+9}=\frac{9}{2}\)
\(\Leftrightarrow\frac{90\left(x+9\right)}{x\left(x+9\right)}+\frac{90x}{x\left(x+9\right)}=\frac{9}{2}\)
\(\Leftrightarrow\frac{90x+810+90x}{x\left(x+9\right)}=\frac{9}{2}\)
\(\Leftrightarrow\frac{180x+810}{x\left(x+9\right)}=\frac{9}{2}\)
\(\Rightarrow2\left(180x+810\right)=9x\left(x+9\right)\)
\(\Leftrightarrow360x+1620=9x^2+81x\)
\(\Leftrightarrow9x^2+81x-360x-1620=0\)
\(\Leftrightarrow9x^2-279x-1620=0\)
\(\Leftrightarrow9\left(x^2-31x-180\right)=0\)
\(\Leftrightarrow x^2-31x-180=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=36\left(tm\right)\\x=-5\left(ktm\right)\end{cases}}\)
Vậy vận tốc xe máy lúc đi từ A đến B là: 36km/h.
HL
20 tháng 5 2015
Đặt ẩn x là vận tốc xe máy (x>0)
Lúc đầu đi vs x km/h thì lúc sau là x+9 km/h
Thời gian đi từ A -> B là 90/x thì thời gian từ B -> A là 90/x+9
Đến B còn nghỉ 30p=1/2h
Lập hệ phương trình thời gian:
(90/x)+1/2+(90/x+9)=5
<=> (90/x)+(90/x+9)=5-1/2
<=> (90.(x+9)+90.x)/x.(x+9)=9/2
<=> 90.x+810+90.x=(9/2).x.(x+9)
<=>180.x+810=(9/2)x^2+(81/2).x
<=> 0 = (9/2).x^2 - (279/2).x - 810
Gpt đc x=36 hoặc x=-5( loại vì ko thỏa mãn điều kiện)
Tóm tắt:
\(t=t_1+t_2=1,4h\)
\(v_1=12km/h\)
\(v_2=6m/s=21,6km/h\)
_______________________________
\(s=s_1=s_2=?km\)
Giải:
\(t=t_1+t_2\Leftrightarrow t_1=t-t_2hayt_1=1,4-t_2\left(1\right)\)
Ta có: \(s=s_1=s_2\)
\(\Leftrightarrow v_1.t_1=v_2.t_2\)
Thế \(\left(1\right)\) vào phương trình trên, ta được: \(v_1.\left(1,4-t_2\right)=v_2.t_2\)
\(\Leftrightarrow12.\left(1,4-t_2\right)=21,6.t_2\)
\(\Leftrightarrow16,8-12t_2=21,6t_2\)
\(\Leftrightarrow16,8=33,6t_2\)
\(\Leftrightarrow t_2=0,5\left(h\right)\)
Quãng đường từ A đến B:
\(s=s_1=s_2=v_2.t_2=21,6.0,5=10,8\left(km\right)\)
Vậy ...