a)\(\dfrac{tanA}{tanB}= \dfrac{AB^2+BC^2-AC^2}{AB^2+AC^2-BC^2}\)
b)\(S=2.R^2.sinA.sinB.sinC\)
c)S=\(\dfrac{1}{2}\)\(\sqrt{AB^2.AC^2-(\overrightarrow{AB}.\overrightarrow{AC})}\)
d)BC= AC.cosC+AB.cosC
e)4(\(m_a^2+m_b^2+m_c^2\))=3(\(AB^2+BC^2+AC^2\))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 2 2021
Ta có : \(\dfrac{1}{2}\sqrt{\overrightarrow{AB}^2\overrightarrow{AC}^2-\left(\overrightarrow{AB}.\overrightarrow{AC}\right)^2}\)
\(=\dfrac{1}{2}.\sqrt{AB^2AC^2-\left(AB.AC.CosBAC\right)^2}\)
\(=\dfrac{1}{2}.\sqrt{AB^2AC^2-AB^2.AC^2.Cos^2BAC}\)
\(=\dfrac{1}{2}\sqrt{AB^2AC^2\left(1-Cos^2BAC\right)}\)
Thấy : \(Sin^2a+Cos^2a=1\)
\(\Rightarrow Sin^2a=1-Cos^2a\)
\(\Rightarrow\dfrac{1}{2}\sqrt{AB^2AC^2Sin^2BAC}=\dfrac{1}{2}\left|AB.AC.SinBAC\right|=\dfrac{1}{2}AB.AC.SinBAC=S\)
=> ĐPCM
7 tháng 2 2021
Sao đề là lạ đoạn kia là \(\left(\overrightarrow{AB}.\overrightarrow{AC}\right)^2\)à
AH
Akai Haruma
Giáo viên
24 tháng 9 2017
Lời giải:
Với $I$ là trung điểm của $BC$ thì \(\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
Ta có:
\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{AI}+\overrightarrow{IC}\)
\(=2\overrightarrow{AI}+(\overrightarrow{IB}+\overrightarrow{IC})\)
\(=2\overrightarrow{AI}\)
\(\Rightarrow \overrightarrow{AI}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\) (đpcm)
b) Gọi giao điểm của $AG$ với $BC$ là $T$
\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{AG}+\overrightarrow{GC}\)
\(=2\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{AG}+\overrightarrow{GI}+\overrightarrow{IB}+\overrightarrow{GI}+\overrightarrow{IC}\)
\(=2\overrightarrow{AG}+2\overrightarrow{GI}\)
Theo tính chất đường trung tuyến thì \(\overrightarrow{AG}=2\overrightarrow{GI}\) nên:
\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AG}+\overrightarrow{AG}=3\overrightarrow{AG}\)
\(\Rightarrow \overrightarrow{AG}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\)
4 tháng 10
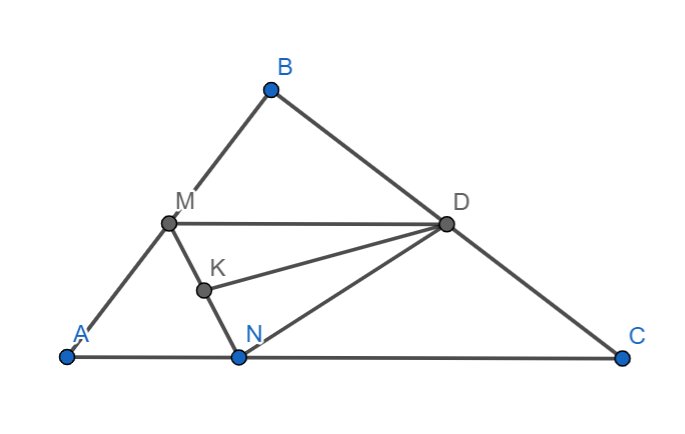
Xét \(\Delta ABC\) có:
\(M\) là trung điểm \(AB\)
\(D\) là trung điểm \(BC\)
\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)
Ta có:
\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)