bài 1
Cho tam giác ABC, AB= AC. M là trung điểm củaBC.Kẻ MH vuông góc với AB, MK vuông góc với AC. Chứng minh rằng:
a) MH=MK
b) Tam giác MHB=tam giác MKC
MK cần gấp lắm. Các bạn giúp mk nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
b: Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)

Tam giác ABC cân tại A=>AM là đường trung tuyến đồng thời là đường phân giác.
=>Góc A1=góc A2.
Xét tam giác vuông AHM và tam giác vuông AKM có:
AM chung.
Góc A1=góc A2.
=>Tam giác AHM=tam giác AKM(cạnh huyền-góc nhọn).
=>AH=AK(2 cạnh tương ứng).
# Aeri #
góc B= góc C => tam giác ABC cân tại A.
M trung điểm BC => AM trung tuyến đồng thời là pg => góc HAM = góc KAM
xét tam giác HAM= tam giác KAM ( cạnh huyền= góc nhọn )
suy ra AH= AK ( dpcm)

a)Ta có: tam giác ABC là tam giác cân
\(=>AB=AC\)
Mà \(AB=4cm\)
=>>AC=4cm
b) Nếu góc B=60 độ =>tgiác ABC là tam giác đèu(t/c)
c) Xét tam giác ABM và tgiác ACM có
AB=AC(cmt)
AM: chung
==>>tgiác ABM=tgiác ACM( ch-cgv)
d) Ta có: tam giác ABM=tgiác ACM(cmt)
=>\(\widehat{AMC}=\widehat{AMB}\)(2 góc tương ứng)
Mà: \(\widehat{AMC+}\widehat{AMC}=180^0\)
\(=>\widehat{AMC=}\widehat{AMB}=\frac{180^0}{2}=90^0\)
=> AMvuông góc vs BC
e) Xét tgiác BMH và tgiác CMK có :
BM=CM( 2 cạnh tương ứng , cmt(a))
\(\widehat{B}=\widehat{C}\)( tgiác ABC là tgiác đều)
==>>>tgiác BMH=tgiác CMK(ch-gn)
=>MH=MK( 2 cạnh tương ứng)

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó; AHMK là hình chữ nhật

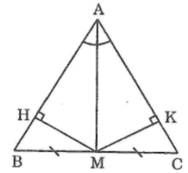
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) =90o
Cạnh huyền AM chung
∠(HAM) =∠(KAM) (gt)
⇒ ΔAHM= ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
Neu ban da hoc tam giac can thi giai nhu sau:
Tam giac ABC can tai A vi AB=AC => B=C
Co: Tam giac MHB vuong tai H
Tam giac MKC vuong tai K
Xet 2 tam giac vuong MHB va MKC co:
MB=MC(gt)
B=C(cmt)
=>Tam giac MHB=Tam giac MKC(canh huyen-goc nhon)
=>MH=MK(2 canh tuong ung)
Bai cua minh con nhieu thieu sot (ki hieu, hinh ve), nho cho * nghen. Thanks!!!