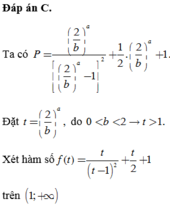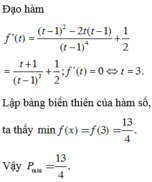cho a,b là hai số dương thỏa mãn \(a+b\le1\).Tìm giá trị nhỏ nhất của biểu thức \(P=a^2b\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
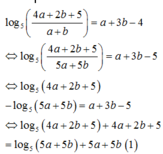
Xét hàm số
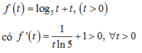
Hàm số f t đồng biến trên 0 ; + ∞
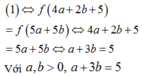
ta có:
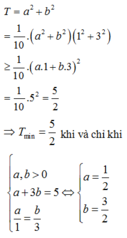
Chọn: D

Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2

Áp dụng bất đẳng thức trên ta có ( 1 + a 2 ) ( 1 + b 2 ) ≥ 1 + a b = 1 + a + b (1)
Với mọi x, y > 0, áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
1 x + 1 y ( x + y ) ≥ 2 1 x . 1 y .2 x y = 4 ⇒ 1 x + 1 y ≥ 4 x + y (2)
Áp dụng (1) và (2) ta có:
P ≥ 4 a 2 + 2 a + b 2 + 2 b + 1 + a + b = 4 a 2 + b 2 + 2 a b + 1 + a + b = 4 ( a + b ) 2 + a + b 8 + 7 ( a + b ) 8 + 1
Áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
a + b = a b ≤ ( a + b ) 2 4 ⇒ ( a + b ) 2 ≥ 4 ( a + b ) ⇒ a + b ≥ 4
Áp dụng bất đẳng thức Côsi cho 2 số dương ta có:
4 ( a + b ) 2 + a + b 16 + a + b 16 ≥ 3 4 ( a + b ) 2 . a + b 16 . a + b 16 3 = 3 4 ⇒ P ≥ 3 4 + 7 8 .4 + 1 = 21 4
Dấu bằng xảy ra khi a = b = 2. Vậy giá trị nhỏ nhất của P là 21/4

Đáp án C.
Ta có P = 2 b a 2 b a − 1 2 + 1 2 . 2 b a + 1. Đặt t = 2 b a , do 0 < b < 2 → t > 1.
Xét hàm số f ( t ) = t t − 1 2 + t 2 + 1 trên 1 ; + ∞ .
Đạo hàm
f ' ( t ) = ( t − 1 ) 2 − 2 t ( t − 1 ) ( t − 1 ) 4 + 1 2 = t + 1 ( t − 1 ) 3 + 1 2 ; f ' ( t ) = 0 ⇔ t = 3.
Lập bảng biến thiên của hàm số, ta thấy min f ( x ) = f ( 3 ) = 13 4 . Vậy P min = 13 4 .

Chỉ làm được 1 tý thôi:
\(a+b+1=8ab\Rightarrow\frac{a+b+1}{ab}=\frac{8ab}{ab}\)
\(\Leftrightarrow\frac{1}{b}+\frac{1}{a}+\frac{1}{ab}=8.\)
Đáp án là 8 á. xảy ra khi a=b=\(\frac{1}{2}\) nhưng mình k biết cách làm.

\(2ab+a+b=2a^2+2b^2\ge2ab+\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\)
\(F=\dfrac{a^4}{ab}+\dfrac{b^4}{ab}+2020\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge\dfrac{\left(a^2+b^2\right)^2}{2ab}+\dfrac{8080}{a+b}\ge a^2+b^2+\dfrac{8080}{a+b}\)
\(F\ge\dfrac{\left(a+b\right)^2}{2}+\dfrac{8080}{a+b}=\dfrac{\left(a+b\right)^2}{2}+\dfrac{4}{a+b}+\dfrac{4}{a+b}+\dfrac{8072}{a+b}\)
\(F\ge3\sqrt[3]{\dfrac{16\left(a+b\right)^2}{\left(a+b\right)^2}}+\dfrac{8072}{2}=...\)