Cho sin a= \(\frac{5}{13}\)(x/2<a<\(\pi\)) Tính tan a+ \(\frac{\pi}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HV
0
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
Ta có:
\(\begin{array}{l}\sin \left( { - \frac{{15\pi }}{2} - \alpha } \right) - \cos \left( {13\pi + \alpha } \right) = \sin \left( { -\frac{{16\pi }}{2} +\frac{{\pi }}{2} + \alpha } \right) - \cos \left( {12\pi + \pi + \alpha } \right) = \sin \left( {-8\pi + \frac{\pi }{2} - \alpha } \right) - \cos \left( { \pi + \alpha } \right) \\ = \sin \left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( \alpha \right) = \cos \left( \alpha \right) + \cos \left( \alpha \right) = 2\cos \left( \alpha \right) = 2.\left( { - \frac{5}{{13}}} \right) = \frac{{ - 10}}{{13}}\end{array}\)
2 tháng 5 2019
\(\cos^2=\frac{1}{1+tan^2x}=\frac{1}{1+25}\\ \Rightarrow cos=\frac{1}{\sqrt{26}}\left(6\pi< x< \frac{13}{2}\right)\)
\(\Rightarrow sin=\frac{5}{\sqrt{26}}\\ \Rightarrow sin2x=2sinxcosx=2\times\frac{5}{\sqrt{26}}\times\frac{1}{\sqrt{26}}=\frac{5}{13}\)
b) \(cos^2=1-sin^2x=\frac{16}{25}\\ \Rightarrow cos=-\frac{4}{5}\left(-\frac{3\pi}{2}< x< -\pi\right)\\\Rightarrow tanx=-\frac{3}{4} \\ tan\left(x-\frac{\pi}{4}\right)=\frac{tanx-tan\frac{\pi}{4}}{1+tanxtan\frac{\pi}{4}}=-7\)
3 tháng 5 2019
6π là số chẵn nên viết được dưới dạng k2π nên nó quay về mức 0 còn \(\frac{13\pi}{2}=\frac{\pi}{2}+6\pi\) nên tóm lại nó lằm từ (0<x<\(\frac{\pi}{2}\))
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a)
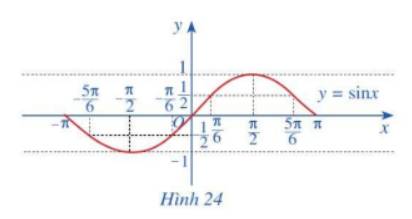
x | \( - \pi \) | \( - \frac{{5\pi }}{6}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{2}\) | \(\frac{{5\pi }}{6}\) | \(\pi \) |
\(y = \sin x\) | 0 | \( - \frac{1}{2}\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 |
b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm \(\left( {x;y} \right)\) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) với nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\)(Hình 24).
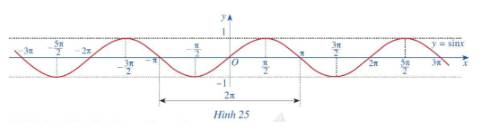
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \sin x\)trên R được biểu diễn ở Hình 25.
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
\(\cos \alpha = - \sqrt {1 - {{\left( { - \frac{5}{{13}}} \right)}^2}} = - \frac{{12}}{{13}}\) (vì \(\pi < \alpha < \frac{{3\pi }}{2}\))
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \sin \alpha \cos \frac{\pi }{6} + \cos \alpha sin\frac{\pi }{6} = \frac{{ - 12 + 5\sqrt 3 }}{{26}}\)
\(\cos \left( {\frac{\pi }{4} - \alpha } \right) = \cos \frac{\pi }{4}\cos \alpha + \sin \frac{\pi }{4}sin\alpha = \frac{{ - 17\sqrt 2 }}{{26}}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2020
\(sin\left(x-\frac{\pi}{2}\right)+sin\frac{13\pi}{2}=sin\left(x+\frac{\pi}{2}\right)\)
\(\Leftrightarrow-cosx+1=cosx\)
\(\Leftrightarrow2cosx=1\Rightarrow cosx=\frac{1}{2}\)
DL
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2019
Ý bạn là \(\pi< a< \frac{3\pi}{2}\) và tìm \(cosa,tana,cota\)?
Khi đó \(cosa< 0\) \(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\frac{12}{13}\)
\(tana=\frac{sina}{cosa}=\frac{5}{12}\)
\(cota=\frac{1}{tana}=\frac{12}{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 7 2020
\(sin\left(x+\frac{\pi}{3}\right)-sin\left(x-\frac{\pi}{3}\right)=sin\left(6\pi+\frac{\pi}{2}\right)\)
\(\Leftrightarrow2cosx.sin\frac{\pi}{3}=sin\left(\frac{\pi}{2}\right)\)
\(\Leftrightarrow2cosx.\frac{\sqrt{3}}{2}=1\)
\(\Rightarrow cosx=\frac{1}{\sqrt{3}}\)