Cho BT
A= +
+
a, tìm điều kiện xác định của x để giá trị của BT xác định
b, Rút gọn BT A
c,tính GT của BT khi x=-4
d, tìm gt nguyên của x để A có gt là số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ: x<>4; x<>-4
b: \(A=\dfrac{\left(x-4\right)\left(x-1\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{x-1}{x+4}\)
c: Để A nguyên thì x+4-5 chia hết cho x+4
=>\(x+4\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{-3;-5;1;-9\right\}\)

\(a,ĐK:x\ne\pm3\\ Sửa:M=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\\ M=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{3\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x-3}\\ b,x=2\Leftrightarrow M=\dfrac{3}{2-3}=-3\\ c,M\in Z\Leftrightarrow x-3\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{0;2;4;6\right\}\left(tm\right)\)

a) ĐKXĐ: \(x\ne\pm1\)
b) \(A=\dfrac{x^3-1}{x^2-1}\cdot\left(\dfrac{1}{x-1}-\dfrac{x+1}{x^2+x+1}\right)\left(dkxd:x\ne\pm1\right)\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\left[\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\right]\)
\(=\dfrac{x^2+x+1}{x+1}\cdot\dfrac{x^2+x+1-\left(x^2-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1-x^2+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x+2}{x^2-1}\)
c) Có: \(\left|x+3\right|=1\Leftrightarrow\left[{}\begin{matrix}x+3=1\\x+3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\left(tmdk\right)\)
+) Với \(x=-2\), thay vào \(A\), ta được:
\(A=\dfrac{-2+2}{\left(-2\right)^2-1}=0\)
+) Với \(x=-4\), thay vào \(A\), ta được:
\(A=\dfrac{-4+2}{\left(-4\right)^2-1}=-\dfrac{2}{15}\)
\(\text{#}Toru\)

a. ĐKXĐ: x \(\ne\pm3\)
b. M = \(\frac{3}{x-3}+\frac{6x}{x^2-9}+\frac{x}{x+3}\)
= \(\frac{3\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\frac{6x}{\left(x-3\right)\left(x+3\right)}+\frac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
= \(\frac{3x+9+6x+x^2-3x}{\left(x-3\right)\left(x+3\right)}\) = \(\frac{9+6x+x^2}{\left(x-3\right)\left(x+3\right)}\)= \(\frac{\left(x+3\right)^2}{\left(x-3\right)\left(x+3\right)}=\frac{x+3}{x-3}\)
c. M = 0 hay \(\frac{x+3}{x-3}=0\) => x + 3 = 0 <=> x = -3 (Loại)

a) Phân thức A được xác định khi: \(x^2-1\ne0\Rightarrow\left(x-1\right)\left(x+1\right)\ne0\Rightarrow\left\{{}\begin{matrix}x+1\ne0\\x-1\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
Vây ĐKXĐ của A là \(\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
b)Ta có: \(A=\dfrac{x^2+2x+1}{x^2-1}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x+1\right)}{\left(x-1\right)}\)
Vậy \(A=\dfrac{x+1}{x-1}\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\)
c) Ta có A=2 <-> \(\dfrac{x+1}{x-1}=2\Leftrightarrow x+1=2\left(x-1\right)\Leftrightarrow x+1=2x-2\)
\(\Leftrightarrow x+1-2x+2=0\Leftrightarrow3-x=0\Rightarrow x=3\)
Vậy khi x=3 thì A=2

a: \(P=\dfrac{x^2+6x+9-x^2+6x-9-4}{\left(x-3\right)\left(x+3\right)}:\dfrac{3x-1}{x-3}\)
\(=\dfrac{4\left(3x-1\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{3x-1}=\dfrac{4}{x+3}\)

a: ĐKXĐ: \(x\notin\left\{0;-1;1\right\}\)
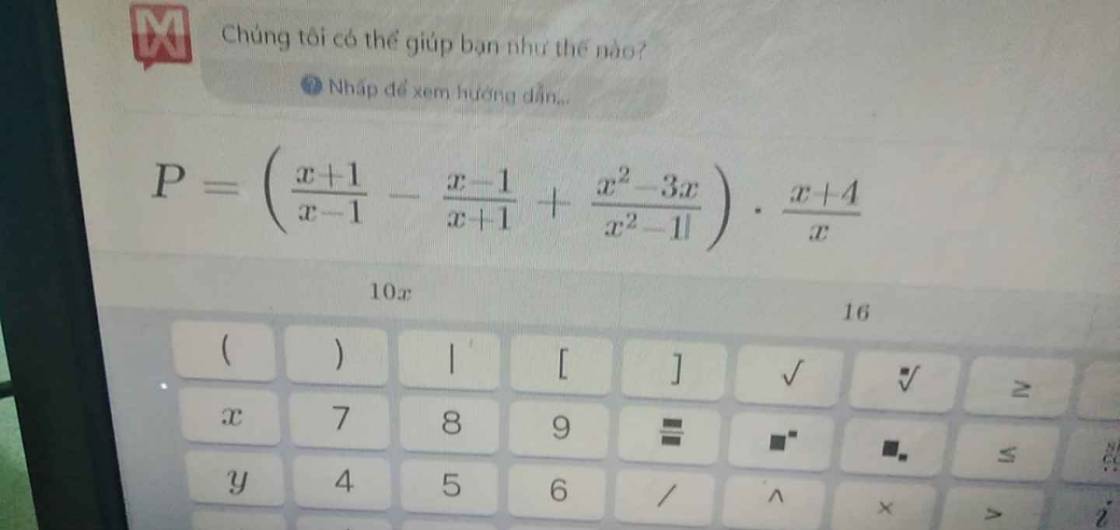
b: \(P=\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}+\dfrac{x^2-3x}{x^2-1}\right)\cdot\dfrac{x+4}{x}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-1\right)^2+x^2-3x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+4}{x}\)
\(=\dfrac{x^2+2x+1-x^2+2x-1+x^2-3x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+4}{x}\)
\(=\dfrac{x^2+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+4}{x}=\dfrac{x+4}{x-1}\)
c: Để P là số nguyên thì \(x+4⋮x-1\)
=>\(x-1+5⋮x-1\)
=>\(5⋮x-1\)
=>\(x-1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{2;0;6;-4\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{2;6;-4\right\}\)

Bài làm
\(P=\frac{x+2}{x+3}-\frac{5}{x^2+x-6}+\frac{1}{2-x}\)
a) ĐKXĐ : \(\hept{\begin{cases}x\ne-3\\x\ne2\end{cases}}\)
\(=\frac{x+2}{x+3}-\frac{5}{x^2+3x-2x-6}-\frac{1}{x-2}\)
\(=\frac{x+2}{x+3}-\frac{5}{x\left(x+3\right)-2\left(x+3\right)}-\frac{1}{x-2}\)
\(=\frac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\frac{5}{\left(x+3\right)\left(x-2\right)}-\frac{x+3}{\left(x+3\right)\left(x-2\right)}\)
\(=\frac{x^2-4}{\left(x+3\right)\left(x-2\right)}-\frac{5}{\left(x+3\right)\left(x-2\right)}-\frac{x+3}{\left(x+3\right)\left(x-2\right)}\)
\(=\frac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\)
\(=\frac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\)
\(=\frac{x^2-4x+3x-12}{\left(x+3\right)\left(x-2\right)}\)
\(=\frac{x\left(x-4\right)+3\left(x-4\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\frac{\left(x-4\right)\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\frac{x-4}{x-2}\)
b) x2 - 9 = 0 <=> ( x - 3 )( x + 3 ) = 0
<=> \(\orbr{\begin{cases}x=3\left(nhan\right)\\x=-3\left(loai\right)\end{cases}}\)
x = 3 => \(P=\frac{3-4}{3-2}=-1\)
c) \(P=\frac{x-4}{x-2}=\frac{x-2-2}{x-2}=1-\frac{2}{x-2}\)
Để P đạt giá trị nguyên => \(\frac{2}{x-2}\)nguyên
=> \(2⋮x-2\)
=> \(x-2\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| x-2 | 1 | -1 | 2 | -2 |
| x | 3 | 1 | 4 | 0 |
Vậy ...
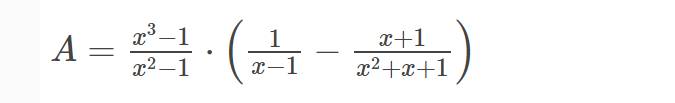
 a) Viết điều kiện xác định
a) Viết điều kiện xác định
βbhgfcvzxcxxcvxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcxcvxcxfc