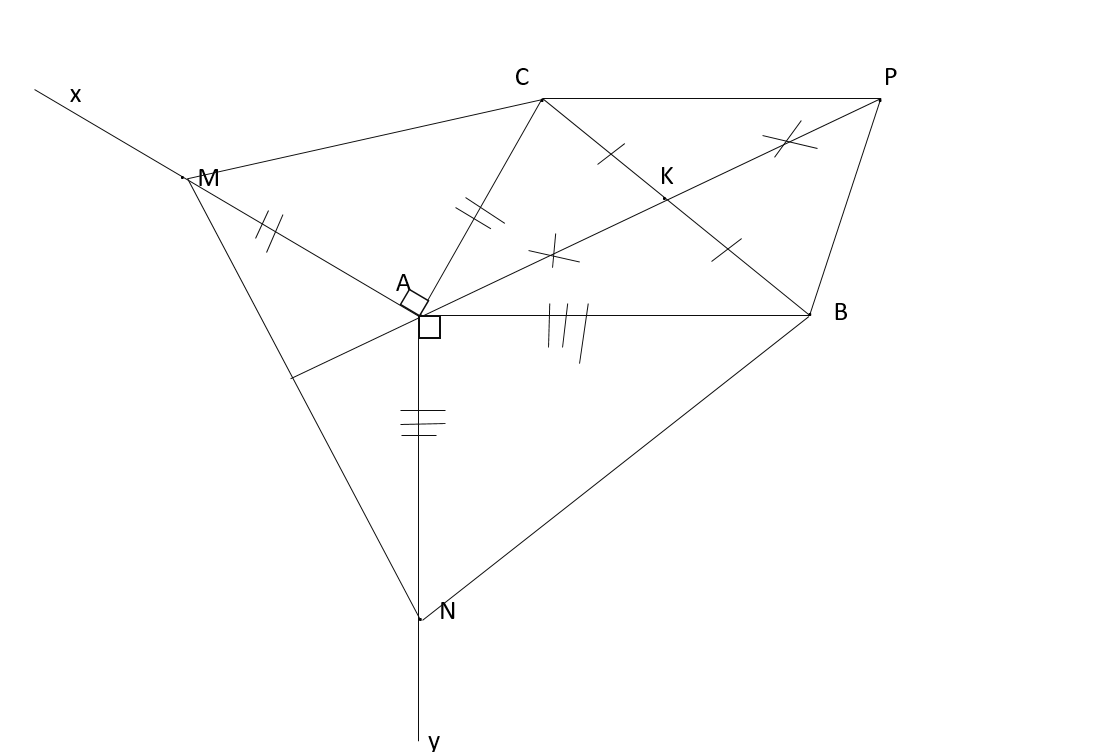
Cho tam giác ABC vuông tại A. Kẻ đường cao AH, từ H kẻ HI//AC
(I thuộc BA) và HK // AB (K thuộc AC).
a) Tứ giác AIHK là hình gì? Vì sao?
b) Trên nửa mặt phẳng bờ AC không chứa điểm B, kẻ tia Ax // BC. Trên tia
Ax lấy điểm N sao cho AN = BM (M là trung điểm của BC). Tứ giác AMCN là hình
gì? Vì sao?
c) Chứng minh AM vuông góc với IK.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
H là trung điểm của BC
HI//AB
Do đó: I là trung điểm của AC
hay AI=IC
b: Xét tứ giác ABCQ có
CQ//AB
CQ=AB
Do đó; ABCQ là hình bình hành
Su ra: AQ//BC

a) dien h tam giac ABC la :S ABC =1/2 AB * AC = 1/2* 6 *8 = 24(m2)
b) Tu giac AIHK co :
goc AIH = goc HKA = goc KAI = 90 do
suy ra AIKH la hinh chu nhat
c)Tu giac AHMD co :
AK = KM
KH=KD
suy ra AHMD la hinh binh hanh
ma goc HKC = 90 do
suy ra AHMD la hinh thoi
c) Trong tam AHC vuong tai H co :
KH la trung tuyen
suy ra KH = 1/2 AC
Chung minh tuong tu ta co : HI = 1/2 AB
De IHKA la hinh vuong thi IH = HK
ma IH = 1/2 AB
KH = 1/2 AC
suy ra AB = AC
suy ra tam giac ABC can
ma tam giac ABC vuong(gt)
suy ra tam giac ABC vuong can
Vay tam giac ABC vuong can thi AIHK la hinh vuong

a: Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=6^2+2^2=40\)
hay \(AB=2\sqrt{10}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=6^2+6^2=72\)
hay \(AC=6\sqrt{2}\left(cm\right)\)

a: Xét tứ giác AIHK có
HK//AI
HI//AK
Do đó: AIHK là hình bình hành
mà \(\widehat{KAI}=90^0\)
nên AIHK là hình chữ nhật