Cho tam giác ABC có Ab = 90◦ , AB < AC. Trên cạnh AC lấy điểm D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. a) Chứng minh rằng DE ⊥ BC.
b) Cho biết 4Bb = 5Cb, tính AED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2023
b,Gọi I là giao điểm của BC và ED
Xét ∆AED và ∆ABC có:
+AB=AD(gt)
+\(\widehat{BAC}=\widehat{DAB}\left(=90^o\right)\)
+AC=AE(gt)
\(\Rightarrow\)∆AED=∆ABC(ch-cgv)
\(\Rightarrow\widehat{EDA}=\widehat{ABC}\) (2 góc tương ứng)
Mà \(\widehat{DEA}+\widehat{EDA}=90^o\)( do ∆ADE vuông tại A)
\(\Rightarrow\widehat{CBA}+\widehat{DEA}=90^o\)
\(\Rightarrow\)∆BIE vuông tại I
\(\Rightarrow DE\perp BC\)
1 tháng 12 2016
\(a.\)
Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(AD=AB\) \(\left(gt\right)\)
\(\widehat{DAE}=\widehat{BAC}\left(=90^0\right)\)
\(AE=AC\) \(\left(gt\right)\)
Do đó : \(\Delta ADE=\Delta ABC\left(c-g-c\right)\)
\(\Rightarrow DE=BC\) ( hai cạnh tương ứng )
\(b.\)
Ta có :
\(\widehat{ADE}=\widehat{CDN}\) ( hai góc đối đỉnh )
\(\widehat{C}=\widehat{E}\) ( vì \(\Delta ADE=\Delta ABC\) )
\(\Rightarrow\widehat{N}=\widehat{A}\left(90^0\right)\)
Hay \(DE\perp BC\)
Vậy \(DE\perp BC\)
21 tháng 2 2021
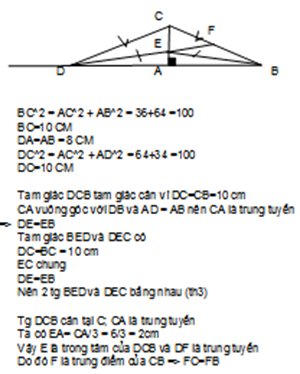
Đáp án:
a) Vì ΔΔABC vuông tại A (Aˆ=90oA^=90o)
=> AB2+AC2=BC2AB2+AC2=BC2 (ĐL Pi-ta-go)
=> BC2=82+62=100BC2=82+62=100
=> BC=10BC=10cm
b) Vì AB = AD (gt)
mà A ∈∈ BD (gt)
=> A trung điểm BD (ĐN trung điểm)
=> CA trung tuyến BD (ĐN trung tuyến)
lại có: CA ⊥⊥ BD (AB ⊥⊥ AC do Aˆ=90oA^=90o)
=> ΔΔCBD cân tại C (dhnb)
=> BC = CD (ĐN ΔΔ cân)
và CA là phân giác của BCDˆBCD^ (t/c ΔΔ cân)
=> C1ˆ=C2ˆC1^=C2^ (ĐN tia p/g)
Xét ΔΔBEC và ΔΔDEC có:
BC = CD (cmt)
C1ˆ=C2ˆC1^=C2^ (cmt)
EC: cạnh chung
=> ΔΔBEC = ΔΔDEC (c.g.c)
c) Vì CE là trung tuyến của ΔΔBCD (cmt)
mà AEAC=26=13AEAC=26=13 (AE = 2cm, AC = 6cm)
=> E là trọng tâm ΔΔBCD (dhnb)
=> DE là trung tuyến ΔΔBCD (ĐN trọng tâm)
=> DE đi qua trung điểm của BC (ĐN trung tuyến)
12 tháng 5 2023
1,3: Xet ΔADE và ΔACB có
AD/AC=AE/AC
góc DAE=góc CAB
=>ΔADE đồng dạng vói ΔACB
=>góc ADE=góc ACB
=>DE//BC
2: DE/CB=AD/AC=3/10
21 tháng 2 2021
Bài 12:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+6^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD(gt)
Do đó: ΔABC=ΔADC(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔEAB vuông tại A và ΔEAD vuông tại A có
EA chung
AB=AD(gt)
Do đó: ΔEAB=ΔEAD(hai cạnh góc vuông)
Suy ra: EB=ED(hai cạnh tương ứng)
Xét ΔCEB và ΔCED có
CE chung
CB=CD(cmt)
EB=ED(cmt)
Do đó: ΔCEB=ΔCED(c-c-c)